5.3. Théorie du chaos et marchés financiers
5.3.1. Les cours de bourses comme objet fractal.
Dans le mouvement brownien avec une distribution de probabilité normale que nous avons analysé plus haut, on a vu que grâce au théorème central limite, on a pu définir une invariance d’échelle au niveau de la distribution. En effet, une distribution normale reste normale quelque soit l’échantillon que l’on prend. Dans le cas d’un mouvement brownien, les accroissements ![]() suivent une loi d’échelle proportionnelle à
suivent une loi d’échelle proportionnelle à ![]() .
.
Donc si on considère X comme étant le cours d’un instrument financier, la distribution de probabilité reste insensible à une variation d’échelle temporelle, il n’y a que son amplitude qui varie de ![]() d’une échelle à l’autre. Ceci signifie que la distribution de probabilité est identique si on travaille sur des cours en intraday, ou si on travaille sur un mois, sur 1 an ou sur 10 ans. Peu importe la période, on a la même distribution en temps de crise qu’en temps de croissance.
d’une échelle à l’autre. Ceci signifie que la distribution de probabilité est identique si on travaille sur des cours en intraday, ou si on travaille sur un mois, sur 1 an ou sur 10 ans. Peu importe la période, on a la même distribution en temps de crise qu’en temps de croissance.
Ainsi, la volatilité d’un actif sur 1 mois est![]() fois moins importante que la volatilité sur 12 mois, soit un rapport de 3,46… Cette conclusion est validée par les observations faites dans la réalité où on arrive à peu près au même résultat. Les cours des changes sont même assez exemplaires à ce niveau comme le montre le graphe de la page suivante qui représente les variations absolues des taux de change Dollar-Deutsche Mark sur une échelle logarithmique :
fois moins importante que la volatilité sur 12 mois, soit un rapport de 3,46… Cette conclusion est validée par les observations faites dans la réalité où on arrive à peu près au même résultat. Les cours des changes sont même assez exemplaires à ce niveau comme le montre le graphe de la page suivante qui représente les variations absolues des taux de change Dollar-Deutsche Mark sur une échelle logarithmique :
A cause de cette invariance d’échelle, on peut considérer le modèle brownien comme une fractale. Dans ces conditions, on pourrait définir à chaque cours une dimension fractale qui pourrait déterminer son degré de volatilité. Il existe cependant des tests complexes qui permettent de donner une probabilité de dimension fractale (algorithme de Grassberger et Procacia). Ces méthodes arrivent à déceler une dimension fractale assez faible mais sont fort approximatifs pour les dimensions fractales plus élevées.
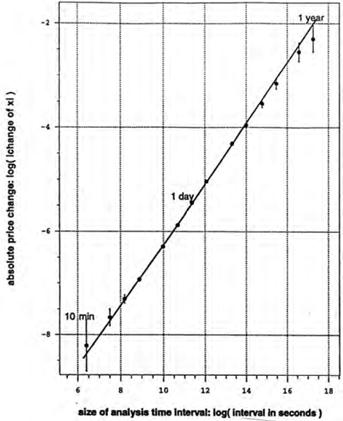
(Source : Christian Walter, Les échelles de temps sur les marchés financiers, Revue de synthèse, 4°S N°1, janv – mars 2001, p55-69)
5.3.2. Les cours de bourses et l’équation logistique.
Nous avons vu ci-dessus comment fonctionnait l’équation logistique qui modélise l’évolution d’une population et nous avons vu que la trajectoire de cette courbe pouvait ressembler étrangement à un cours de bourse. Même si la trajectoire d’un mouvement brownien ressemble à celle d’une équation logistique, l’une est résolument aléatoire et considère les grandes variations comme des évènements survenants au hasard ; tandis que l’autre est totalement déterminée et considère que les grandes variations font partie du modèle et surviennent à des moments déterminés, pas nécessairement cycliques.
Reprenons notre équation logistique :
![]()
Supposons maintenant que µ est une constante qui représente l’environnement économique dans lequel évolue notre action ou, mieux, le niveau d’information que possèdent les acteurs à propos du marché.
Supposons aussi, comme hypothèse forte, que nous avons réussi à nous débarrasser du bruit blanc des marchés pour n’isoler que la tendance générale et que cette tendance peut se décrire à l’aide de notre équation logistique. Cette fonction pourrait nous aider à modéliser la fonction a(x,t) que nous avons utilisé dans le processus d’Îto que nous avons détaillé plus haut.
Dans le cadre de la théorie des marchés efficients décrite plus haut, si l’information disponible reste la même, le prix devrait être constant. Donc µ serait, par exemple, égal à 1,5 avec une valeur fondamentale de 0,33 et la trajectoire aurait cette forme-ci :
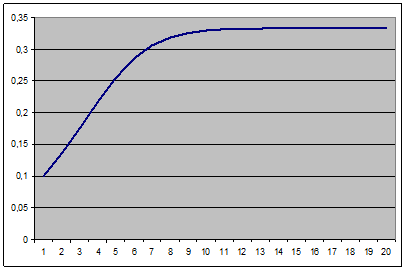
Lorsqu’il y aurait des modifications de l’environnement économique, on pourrait faire varier µ et le prix pourrait évoluer vers un autre niveau. Prenons par exemple notre équation logistique avec µ=1,5 et modifions µ à 2 après 10 itérations. Le prix évoluerait vers un autre niveau de stabilité (ici, 0,5). On aurait la figure suivante :
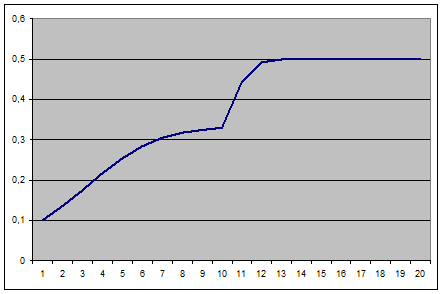
Cependant, si k devient plus élevé, les variations deviennent chaotiques et on a l’impression qu’elles sont générées aléatoirement :
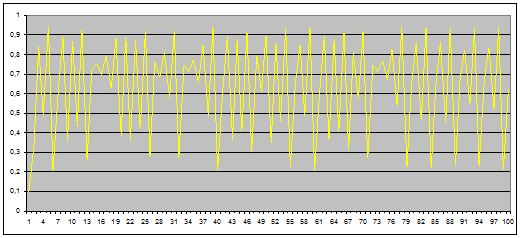
Si il existe une composante chaotique dans les marchés financiers, celle-ci permettrait d’expliquer des mouvements d’ajustement des marchés et certains cycles de ceux-ci ainsi que certains krach. En outre, ce chaos caché pourrait aussi expliquer les phénomènes de mémoire du marché, c’est-à-dire la composante non-aléatoire que nous avons montré au point 4.3.3.4.
5.3.3. Recherche d’attracteurs.
Nous avons vu que les trajectoires des équations logistiques semblaient aléatoires quand µ est au-dessus de 3, ainsi les théoriciens du chaos ont mis au point quelques tests pour différencier un comportement chaotique d’un comportement aléatoire. Nous allons chercher un attracteur dans les équations logistiques.
Une des méthodes utilisées est de reporter les couples de points ![]() sur un graphe à deux dimensions.
sur un graphe à deux dimensions.
Prenons notre équation logistique avec µ = 3,77 et 0,1 comme point de départ. Nous obtenons le graphe suivant qui nous semble aléatoire :
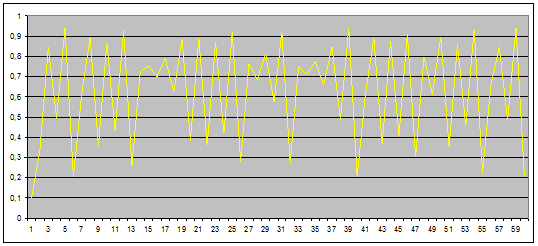
Si nous reportons les points sur un graphe, nous obtenons la courbe suivante :
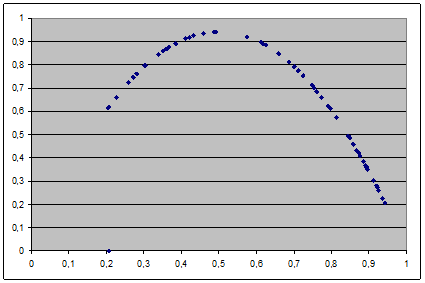
Ceci nous montre que derrière un chaos apparent se cache quelque chose de très ordonné. En fait, il suffit de trouver l’équation de cette courbe pour retomber sur notre équation logistique. Voici le graphe de la courbe d’équation x=3,77 x (1-x) qui correspond parfaitement à notre nuage de points :
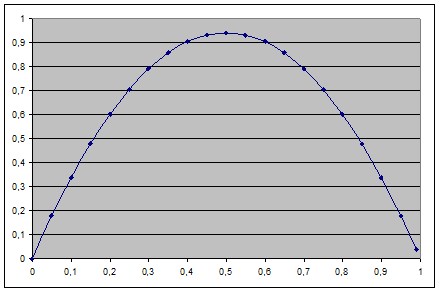
Nous allons appliquer ce procédé à une action pour voir si nous obtenons quelque chose qui ressemble à un attracteur. Pour ce faire, nous allons prendre comme exemple les cours des actions Michelin entre le 1° janvier 2007 et le premier juillet 2007 que vous trouverez dans le fichier _Chaos.xls dans les annexes.
Nous allons tenter de voir ce qui se passe au niveau du volume et des prix. Nous allons donc prendre les points du volume et des prix en nominal et les reporter sur un graphe pour voir si ils convergent vers quelque chose.
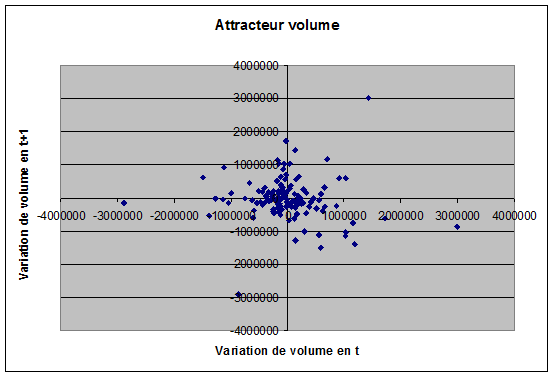
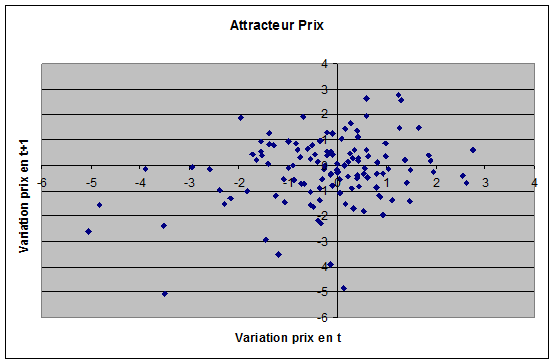
On voit que le point (0,0) pourrait être considéré comme un attracteur mais nous ne voyons pas une forme franche se dégager. Et on ne pourrait pas considérer le point central comme attracteur chaotique.
5.3.4. Difficultés pour détecter un chaos sous-jacent.
Il existe plusieurs méthodes numériques qui permettent de détecter des non linéarités sous-jacentes à des séries de chiffres. Cependant, à ce jour, aucune n’a réussi à confirmer la présence de systèmes non linéaire chaotiques cachés derrière les cours de bourse. Mais aucune méthode n’a réussi à prouver qu’il n’existait pas de systèmes non linéaires.
En fait, la difficulté de cette détection vient du fait que si ce chaos existe, il est mélangé à du bruit blanc. Il est donc très difficile de filtrer ce bruit blanc pour pouvoir en extraire des données exploitables. Il existe bien des méthodes de filtrages mais jusqu’à aujourd’hui, elles ne se sont pas révélées efficaces pour dégager des données susceptibles de montrer une non-linéarité. Ensuite, les méthodes qui permettent de calculer une dimension fractale et de détecter le chaos fonctionnent pour des dimensions fractales faibles. Il se peut donc aussi que le chaos qui se cache derrière les marchés financiers soit assez complexe et de dimension fractale élevée, ce qui rendrait sa détection encore plus difficile.
Aujourd’hui il existe des présomptions de chaos dans les cours de bourse mais il n’existe pas encore de preuve formelle que celui-ci est bien présent.
5.3.5. Les enjeux de l’identification d’un chaos sous-jacent dans les marchés financiers.
La découverte d’un chaos intrinsèque pourrait permettre de construire des modèles financiers beaucoup plus efficaces que ceux qui sont utilisés aujourd’hui et qui sont basés sur des concepts linéaires.
Le chaos sous-jacent pourrait mieux nous faire comprendre le fonctionnement des marchés, leur nature profonde. Aujourd’hui, on est obligé de traiter toutes les grandes variations comme des perturbations extérieures aux modèles qu’il faut ensuite adapter pour qu’ils en tiennent compte. La théorie du chaos pourrait permettre d’avoir un modèle où ces chocs extérieurs ne seraient plus des variables exogènes mais endogènes, faisant partie du modèle à part entière.
5.3.6. Des pistes pour de nouveaux modèles.
Même si en économie, on n’est pas encore arrivé à la faire sortir au grand jour, la théorie du chaos a permis des avancées majeures dans beaucoup de domaines. On a vu qu’on pouvait générer du chaos à partir d’un modèle de distribution de population issu de l’écologie. Il existe d’autres modèles intéressants comme celui de Voltera-Lotka qui est basé sur la relation prédateur-proie. On y modélise l’évolution de la population des prédateurs en fonction de la population des proies et vice-versa. On pourra s’inspirer de ce modèle pour définir une population d’acheteurs et une population de vendeurs, la rencontre de ces deux populations se ferait sur le marché et nous pourrions en tirer une fonction de prix qui utiliserait ces deux populations comme variables.
Lire le mémoire complet ==> (Comparaison épistémologique entre les modèles issus des sciences de la vie et les modèles de valorisation d’actions)
Mémoire présenté pour l’obtention du grade de Master en sciences commerciales
Enseignement supérieur de type long de niveau universitaire
Groupe ICHEC – ISC St-LOUIS – ISFSC – Haute Ecole

