5.4. Décodage épistémologique sur la théorie du chaos
La théorie du chaos fonctionne à l’inverse des théories quantiques. En mécanique quantique, on part de postulats selon lesquels la situation d’origine est estimée de façon probabiliste et on essaye de faire des prédictions quant à son comportement. En théorie du chaos, on a une situation de départ connue, déterminée mais on n’arrive pas à faire des prédictions sur le comportement futur.
Pire, selon cette théorie, il est impossible de faire des prévisions à plus ou moins long terme. En fait, on dispose d’un horizon limité dans lequel les prévisions qu’on fait sont respectées avec une marge d’erreur définie.
Ce n’est pas un hasard si la naissance de la théorie du chaos coïncide avec l’avènement de l’informatique. En effet, ce n’est qu’à partir du moment où les scientifiques ont pu bénéficier d’une puissance de calcul intéressante qu’ils ont commencé à pouvoir explorer facilement des domaines où avant, avec une feuille et un crayon, ils étaient réduits à faire des extrapolations et des simplifications.
On a vu l’extrême sensibilité des équations non linéaire aux conditions initiales, on s’est rendu compte qu’on pouvait avoir de grandes variations en modifiant une décimale quatre chiffres derrière la virgule.
Il existe donc des limites au calcul informatique puisque celui-ci ne pouvant pas manipuler des nombres de longueur infinie, il tronque ses résultats à un certain nombre de décimales. Et donc, à chaque étape des calculs, il en tronque le résultat et donc augmente l’erreur due à la sensibilité aux conditions initiales. Nous voilà réduit comme les météorologues à revoir nos calculs au fur et à mesure que nous recevons de nouvelles mesures afin d’essayer de coller au mieux à la réalité tout en sachant que nous n’y arriverons jamais.
En ce sens, grâce à l’évolution informatique, on se rend compte qu’il existe des problèmes de calculs entre les modèles et la réalité. Ceci détruit encore un peu plus la vision déterministe du monde puisqu’on s’est rendu compte que même les équations phares du déterminisme que sont les équations de Newton décrivant la trajectoire des planètes, étaient soumises au chaos et qu’au delà d’un certain horizon, elles n’étaient plus fiables.
On sait aujourd’hui que l’équation de la trajectoire de la terre dans notre système solaire n’est juste que dans un certain horizon et que les trajectoires des planètes sont chaotiques. Nous connaissons aujourd’hui la position de notre planète avec une précision de 15 mètres, ce qui est ridiculement petit à l’échelle du système solaire. Il a été calculé que la marge d’erreur monte à 150 mètres si on cherche à connaître la position de la terre dans 10 millions d’années, ce qui reste une erreur encore très acceptable. Par contre, passé le cap des 10 millions d’années, l’incertitude augmente de façon exponentielle.
Cette incertitude monte à 150 millions de km à un horizon de 100 millions d’années, soit la distance terre-soleil. Ce qui signifie que nous sommes incapables de prévoir la position de notre planète au delà de 10 millions d’années. Selon Prigogine, le théorie du chaos démonte l’idée de ligne du temps chère aux déterministes. Non seulement nous ne pouvons pas prédire le futur, mais nous ne pouvons pas non plus déduire le passé.
Un autre intérêt de la théorie du chaos est que nous nous intéressons à un phénomène dans toute sa globalité. Contrairement aux théories déterministes qui consistaient à réduire un phénomène en différentes parties et puis modéliser chaque partie séparément et réassembler le tout en tentant d’expliquer le phénomène global, la théorie du chaos essaye de décrire un phénomène dans son ensemble.
Trop souvent les théories déterministes écartaient des phénomènes observés qu’elles ne pouvaient expliquer, car trop désordonnés, en arguant des phénomènes de bruit blanc ou de parasites. Alors que justement ces observations rapportaient des phénomènes réels et qui peuvent maintenant être expliqués par des nouvelles théories.
Ceci dit, il ne faut pas crier victoire trop tôt. En effet, même si la théorie du chaos permet d’expliquer des phénomènes aux allures désordonnées, il existe encore des phénomènes de bruit blanc qui peuvent se mélanger à des perturbations chaotiques rendant la chose extrêmement difficile à détecter. Il existe des tests mathématiques assez sophistiqués qui peuvent arriver à séparer ce qui relève purement du hasard et ce qui relève de perturbations chaotiques.
C’est notamment le cas, malheureusement, pour beaucoup de tentatives de modélisations financières. Si on arrive à quelques résultats prometteurs dans des domaines comme le marché des devises ou les cycles économiques, force est de constater qu’il n’existe encore aucun modèle pour le marché des actions.
Conclusion générale :
Nous avons cherché à mieux comprendre les modèles utilisés pour évaluer des entreprises et l’évolution de ces modèles. Pour ce faire, nous avons utilisé l’épistémologie afin de pouvoir comparer les sciences de la vie avec la science économique. Nous avons vu que l’épistémologie avait aussi évoluée et qu’aujourd’hui elle s’oriente plutôt vers la pensée réaliste.
Grâce à ces comparaisons, nous avons pris conscience que les modèles utilisés pour faire des prédictions de cours d’action ou de valorisation ne sont utilisables qu’au prix de lourdes hypothèses.
Dans le cas du modèle de Gordon-Shapiro, nous avons dû estimer une suite d’augmentation constante de dividendes, dans le cas du modèle inspiré du mouvement brownien, nous avons dû considérer que les cours étaient distribués indépendamment selon une distribution normale et dans le cas de modèles inspirés par la théorie du chaos, nous sommes réduit à chercher un modèle débarrassé de ses bruits blancs qui sont supposés le masquer. Dans tous les cas, nous devons nous écarter de la réalité pour concevoir des modèles utilisables mais qui ne sont, dès lors, plus que le reflet de la réalité.
En fait, l’épistémologie nous dit que quelque soit le modèle, celui-ci n’est qu’une construction mathématique qui tente de décrire la réalité. Mais cette réalité est insaisissable et aucun modèle ne pourrait bien en rendre compte. Il faut, en outre, connaître la façon dont ils sont construits pour pouvoir en déceler les faiblesses et les limites.
Ensuite, nous utilisons ces modèles pour nous donner des indications sur ce que nous cherchons à savoir. Le problème est que trop souvent, à force d’utiliser ces modèles, nous avons tendance à les confondre avec la réalité et à en oublier les conséquences de leurs faiblesses.
Aujourd’hui, le secteur bancaire est soumis aux protocoles décrits dans les accords de Bâle II. Ces protocoles décrivent les outils mathématiques à utiliser pour assurer la solvabilité des banques en cas de crise. Or, on l’a vu, ces protocoles utilisent des modèles basés sur le mouvement brownien avec une distribution normale que nous avons pu étudier ici.
Nous avons vu que pour réaliser ce modèle, nous avions dû poser des hypothèses très fortes comme le fait que les cours soient distribués normalement ou que ces cours sont indépendants les uns des autres. Or, nous avons vu que ces cours avaient une mémoire et que cette mémoire pouvait influencer très fortement la façon dont bougeaient les cours.
Pour avoir un modèle efficace, il faudrait pouvoir étudier et modéliser la façon dont cette mémoire agit sur les cours. Dès lors, on se rend compte que les modèles sur lesquels se basent la plupart des établissements financiers pour assurer leur solvabilité manquent de réalisme. Ces modèles sont fiables lorsqu’il s’agit de modéliser le cours normal d’une action mais ne sont plus fiables du tout lorsqu’il s’agit de rendre compte des phénomènes d’emballements ou de crises.
Nous avons vu au début de notre exposé comment s’étaient déroulées les précédentes crises financières et nous avons vu qu’à chaque fois, une des causes de ces crises étaient des modèles défaillants.
Aujourd’hui, alors que nous subissons toujours la crise des subprimes, nous avons vu la faillite de plusieurs banques comme Northern Rock, Bear Sterns, Indymac, etc. Tandis que d’autres grandes banques sont obligées de faire de colossales augmentations de capital pour couvrir leurs pertes, à l’instar de Fortis en Belgique.
Or c’est ce genre de situation que Bâle II est sensé éviter. Il apparaît de plus en plus clairement que les modèles à distribution normale utilisés en stress testing par les banques manquent de fiabilité quant aux emballements des crises et donc peuvent mettre en péril leur solvabilité. De plus, les modèles utilisés n’intègrent pas non plus la notion de mémoire du marché et donc ne sont pas aptes à prévoir des situations qui arrivent vraiment dans la réalité.
On peut aussi légitimement se poser la question de savoir si les banques n’ont pas intérêt à utiliser des modèles qui ne reflètent pas complètement la réalité dans la mesure où, pour une banque, il est économiquement intéressant de minimiser les fonds propres tout en maximisant les crédits qu’elle accorde, et donc d’utiliser les modèles qui valident la plus petite quantité de fonds propres nécessaires pour être en conformité avec la législation.
Nous avons aussi vu qu’il était impossible de réaliser un modèle prédictif réellement fiable à long terme et que selon les préceptes de la théorie du chaos, les modèles que nous pouvons utiliser n’ont une validité que jusqu’à un certain horizon. Au delà, les imprécisions des données de départ sont telles que le modèle divergerait largement. Il est donc totalement utopique de faire confiance à des modèles de prévision au-delà d’un certain horizon.
Donc finalement, si nous devions nous fier aux modèles que nous utilisons, le comportement des marchés ne serait jamais prévisible ou au maximum prévisibles comme l’est la météo. Heureusement, ces modèles sont décalés par rapport à la réalité et c’est ce qui permet aux marchés de fonctionner et aux acteurs financiers d’espérer pouvoir gagner de l’argent.
Glossaire
Action : Une action est un titre de prorpiété qui correspond à une partie d’une entreprise.
Bruit blanc : Un bruit blanc est un processus stochastique qui possède la même densité spectrale de puissance à toutes les fréquences. Ceci correspond à une autocorrélation nulle en tout point.
Falsification : il s’agit en fait d’un processus de réfutabilité auquel s’expose toute science. La falsification a pour but de mettre une théorie à l’épreuve de l’expérience. Si l’expérience ne suit pas ce que la théorie prédit, on peut alors en conclure que la théorie est fausse. Le fait qu’on ne puisse pas falsifier une théorie aujourd’hui, n’implique pas qu’on ne puisse le faire plus tard. Entre-temps, la théorie est considérée comme correcte. Une falsification peut aussi restreindre le champ d’application d’une théorie. Celle-ci sera considérée comme correcte sur un certain domaine et fausse sur un autre domaine.
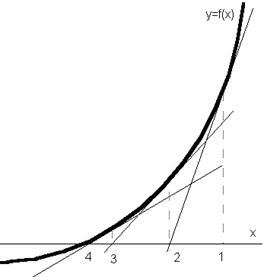
Méthode de Newton-Raphson : méthode de calcul numérique qui permet de trouver les racines d’une équation par itérations. Elle consiste à prendre la tangente à la courbe, de croiser cette tangente avec l’axe des x et d’utiliser la valeur d’intersection pour calculer un nouvel y à partir duquel on retrace une tangente, etc. En principe, les itérations convergent assez rapidement vers la racine de l’équation. Mais il peut arriver que pour certaines équations, le procédé diverge.
Mole : La mole est la quantité de matière d’un système contenant autant d’entités élémentaires qu’il y a d’atomes dans 12 grammes de carbone 12. Une mole d’atomes contient environ atomes
Nucléon : partie d’un atome. Peut-être soit un neutron, soit un proton
Processus de Markov : Processus dont l’état présent est indépendant des états antérieurs. Une chaîne de Markov est un Processus de Markov discret.
Processus Stochastique : Un processus stochastique est «un procédé de définition d’une fonction X(t) du temps t dans lequel le hasard intervient à chaque instant, quelque soit la valeur de t que l’on considère»
Lire le mémoire complet ==> (Comparaison épistémologique entre les modèles issus des sciences de la vie et les modèles de valorisation d’actions)
Mémoire présenté pour l’obtention du grade de Master en sciences commerciales
Enseignement supérieur de type long de niveau universitaire
Groupe ICHEC – ISC St-LOUIS – ISFSC – Haute Ecole

