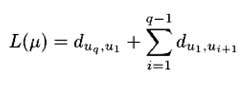META-HEURISTIQUES D’OPTIMISATION PAR COLONIE DE FOURMIS POUR LA RESOLUTION DE PROBLEME DE VOYAGEURS DE COMMERCE BI-OBJECTIFS – CHAPITRE IV :
I. INTRODUCTION :
II. POURQUOI LES FOURMIS :
III. RELATION AVEC L’INFORMATIQUE
IV. COMPORTEMENT DE LA FOURMI :
V. SIMILARITES ET DEFERENCES ENTRE LES FOURMIS ARTIFICIELLES ET LES FOURMIS REELLES :
V.1 POINTS COMMUNS :
V.2. DEFERENCES :
VI. ALGORITHME ANT SYSTEM (AS) : [16]
VI.1. DEfiNITION
VI.2. ANT SYSTEM :
VI.2.1. Conventions
VI.2.2. Choix d’implémentation :
VI.3. FONCTIONNEMENT DE L’ALGORITHME :
VII. L’ALGORITHME BICRITERIONANT
VIII. ALGORITHME PROPOSE POUR BI-OBJECTIFS:
VIII.1. LES FORMULES
IX. CONCLUSION
I. Introduction :
La méta-heuristique d’optimisation par colonie de fourmis est relativement récente. Elle a été introduite en 1991 par Colorni, Dorigo et Maniezzo pour résoudre le problème du Voyageur de commerce. Elle s’est popularisée, puis a été l’objet d’améliorations dès 1995 et a été appliquée avec succès à d’autres problèmes d’optimisation combinatoire dès 1994.
Les algorithmes de colonies de fourmis sont nés à la suite d’une constatation : les insectes sociaux en général, et les fourmis en particulier, résolvent naturellement des problèmes relativement complexes. Les biologistes ont étudié comment les fourmis arrivent à résoudre collectivement des problèmes trop complexes pour un seul individu, notamment les problèmes de choix lors de l’exploitation de sources de nourriture.
Les fourmis sont pas comme d’autre insectes sociaux sa soit de sont comportement social ou de sont organisation, sont développement très avancées est résulte le partage de leur activités de production « recherche de la nourriture, défense de nid, entretien, la constriction de nid et entretien des larves et leur approvisionnement en nourriture » touts ces activités ont importantes pour le développement et la survie de la colonie, ces activités ont une relation directe avec le temps et l’environnement.
II. Pourquoi les fourmis :
Le comportement des fourmis est un comportement collectif. Chaque fourmi a pour priorité le bien être de la communauté.
Chaque individu de la colonie est à priori indépendant et n’est pas supervisé d’une manière ou d’une autre. Ce concept est appelé Hétérarchie (s’opposant à la Hiérarchie), chaque individu est aidé par la communauté dans son évolution et en retour il aide au bon fonctionnement de celle-ci.
La colonie est donc auto-contrôlée par le biais de mécanismes relativement simples à étudier.
III. Relation avec l’informatique :
En observant une colonie de fourmis à la recherche de nourriture dans les environs du nid, on s’aperçoit qu’elle résoudre des problèmes tels que celui de la recherche du plus court chemin.
Les fourmis résolvent des problèmes complexes par des mécanismes assez simples à modéliser.
Leur technique repose sur la pose de marqueurs chimiques, les phéromones, déposés sur les trajets parcourus. Cela peut paraître surprenant au premier abord mais un chemin plus court reçoit plus de phéromones qu’un chemin plus long. Les fourmis suivantes ayant tendance à emprunter les chemins les plus marqués, une solution va progressivement se dessiner.
Il est ainsi assez simple de simuler leur comportement par des algorithmes.
IV. Comportement de la fourmi :
Les pistes de phéromones :
En marchant du nid à la source de nourriture et vice-versa (ce qui dans un premier temps se fait essentiellement de façon aléatoire), les fourmis déposent au passage sur le sol une substance odorante appelée phéromones. Cette substance permet ainsi donc de créer une piste chimique, sur laquelle les fourmis s’y retrouvent, en effet, d’autres fourmis peuvent détecter les phéromones grâce à des capteurs sur leurs antennes.
Les phéromones ont un rôle de marqueur de chemin: quand les fourmis choisissent leur chemin, elles ont tendance à choisir la piste qui porte la plus forte concentration de phéromones. Cela leur permet de retrouver le chemin vers leur nid lors du retour. D’autre part, les odeurs peuvent être utilisées par les autres fourmis pour retrouver les sources de nourritures trouvées par leurs congénères.
Ce comportement permet de trouver le chemin le plus court vers la nourriture lors que les pistes de phéromones sont utilisées par la colonie entière. Autrement dit, lorsque plusieurs chemins marqués sont à la disposition d’une fourmi, cette dernière peut connaitre le chemin le plus court vers sa destination. Cette constatation essentielle est la base de toutes les méthodes que l’on va développer plus loin.
On va d’abord étudier le comportement naturel de ces individus afin d’en prouver la validité, avant de l’extraire pour le simuler informatiquement. [14]
V. Similarités et déférences entre les fourmis artificielles et les fourmis réelles :
Les fourmis artificielles ont une double nature. D’une part, elles modélisent les comportements abstraits de fourmis réelles, et d’autre part, elles peuvent être enrichies par des capacités que ne possèdent pas les fourmis réelles, afin de les rendre plus efficaces que ces dernières. Nous allons maintenant synthétiser ces ressemblances et déférences. [15]
V.1 Points communs :
Colonie d’individus coopérants :
Comme pour les fourmis réelles, une colonie virtuelle est un ensemble d’entités non-synchronisés, qui se rassemblent ensemble pour trouver une «bonne» solution au problème considéré. Chaque groupe d’individus doit pouvoir trouver une solution même si elle est mauvaise.
Pistes de phéromones :
Ces entités communiquent par le mécanisme des pistes de phéromone. Cette forme de communication joue un grand rôle dans le comportement des fourmis : son rôle principal est de changer la manière dont l’environnement est perçu par les fourmis, en fonction de l’historique laissé par ces phéromones.
Évaporation des phéromones :
La méta-heuristique ACO comprend aussi la possibilité d’évaporation des phéromones. Ce mécanisme permet d’oublier lentement ce qui s’est passé avant. C’est ainsi qu’elle peut diriger sa recherche vers de nouvelles directions, sans être trop contrainte par ses anciennes décisions.
Recherche du plus petit chemin :
Les fourmis réelles et artificielles partagent un but commun : recherche du plus court chemin reliant un point de départ (le nid) à des sites de destination (la nourriture). Déplacement locaux Les vraies fourmis ne sautent pas des cases, tout comme les fourmis artificielles, elles se contentent de se déplacer entre sites adjacents du terrain.
Choix aléatoire lors des transitions.
Lorsqu’elles sont sur un site, les fourmis réelles et artificielles doivent décider sur quel site adjacent se déplacer. Cette prise de décision se fait au hasard et dépend de l’information locale déposée sur le site courant. Elle doit tenir compte des pistes de phéromones, mais aussi du contexte de départ (ce qui revient à prendre en considération les données du problème d’optimisation combinatoire pour une fourmi virtuelle).
V.2. Déférences :
Les fourmis artificielles possèdent certaines caractéristiques que ne possèdent pas les fourmis réelles : Elles vivent dans un monde non-continu. Leurs déplacements consistent en des transitions d’état.
Mémoire (état interne) de la fourmi :
Les fourmis réelles ont une mémoire très limitée. Tandis que nos fourmis artificielles mémorisent l’historique de leurs actions. Elles peuvent aussi retenir des données supplémentaires sur leurs performances.
Nature des phéromones déposées :
Les fourmis réelles déposent une information physique sur la piste qu’elles parcourent, là où les fourmis artificielles modifient des informations dans les variables d’états associées au problème. Ainsi, l’évaporation des phéromones est une simple décrémentation de la valeur des variables d’états à chaque itération.
Qualité de la solution :
Les fourmis artificielles déposent une quantité de phéromone proportionnelle à la qualité de la solution qu’elles ont découverte.
Retard dans le dépôt de phéromone :
Les fourmis artificielles peuvent mettre à jour les pistes de phéromones de façon non immédiate : souvent elles attendent d’avoir terminé la construction de leur solution. Ce choix dépend du problème considéré bien évidemment.
Capacités supplémentaires :
Les fourmis artificielles peuvent être pourvues de capacités artificielles afin d’améliorer les performances du système. Ces possibilités sont liées au problème et peuvent être :
- 1. l’anticipation : la fourmi étudie les états suivants pour faire son choix et non seulement l’état local.
- 2. le retour en arrière : une fourmi peut revenir à un état déjà parcouru car la décision qu’elle avait prise à cet état a été mauvaise.
VI. Algorithme Ant System (AS) : [16]
VI.1. Définition :
Données fournies :
- – un ensemble fini X de noeuds représentant des villes
- – un ensemble fini U={(i,j)|i,j ∈X} d’arcs reliant les noeuds de X
- – un ensemble de constantes dij représentant la longueur de chaque arc (i,j)∈ U , c’est-à-dire la distance séparant la ville i de la ville j (avec i,j ∈ X).
On imagine alors un voyageur de commerce qui doit réaliser sa tournée en visitant une et une seule fois l’ensemble X des villes. Il souhaite déterminer la suite de villes qui minimisera la distance qu’il a à parcourir.
Formalisation :
- – circuit hamiltonien est un circuit qui passe exactement une fois par tous les sommets du graphe.
- – la longueur d’un circuit µ est la somme des longueurs des arcs qui le composent, soit :

- – le TSP (Traveling Salesman Problem) est le problème consistant à trouver un circuit hamiltonien de longueur minimale sur le graphe G = (X,U).
Le voyageur de commerce est un problème NP-complet. La métaphore de la colonisation de fourmis s’y applique particulièrement bien.
VI.2. Ant System :
VI.2.1. Conventions :
Ant System sera par la suite appelé AS. Les variables que nous devons définir pour comprendre la suite sont les suivantes :
- – bi(t)(ou i ∈ X) le nombre de fourmis dans la ville i à l’instant t
- – m=∑ i∈ X bi leur nombre total, invariant dans le temps
- – τij(t) la valeur de τij , à l’instant t
- – n = |X|, le nombre de villes
- – ηij = 1/dij, la visibilité d’une ville j quand on est placé sur la ville i, invariante dans le temps.
Précisons maintenant le comportement de l’ensemble de la colonie. A tout instant t, chaque fourmi choisit une ville de destination selon un choix défini. Toutes les fourmis se placent à l’ instant t+1dans une ville de leur choix.
On appelle une itération de l’algo AS, l’ensemble de déplacements de l’ensemble de la colonie entre l’instant t et l’instant t+1. Ainsi après n itérations, l’ensemble de la colonie aura effectué un circuit hamiltonien sur le graphe. De cette manière toutes les fourmis commenceront et finiront leur tour en même temps.
VI.2.2. Choix d’implémentation :
On précise que chaque fourmi a une mémoire implémentée par une liste de villes déjà visitées. Cela permet de garantir qu’aucune fourmi ne visitera deux fois une même ville au cour de sa recherche.
La mémoire de chaque fourmi est vidée lorsqu’elles ont terminé leur cycle.
Choix des transitions
Une fourmi k placée sur la ville i à l’instant t va choisir sa ville j de destination en fonction de la visibilité ηij de cette ville et de la quantité de phéromones τij(t) déposée sur l’arc reliant ces deux villes. Ce choix sera réalisé de manière aléatoire, avec une probabilité de choisir la ville j donnée par :
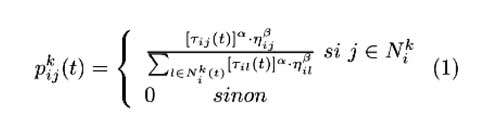
Où l’on défini l’ensemble NKi comme étant l’ensemble des villes que la fourmi k, placée sur la ville i, n’a pas encore visité à l’instant t dans le cycle courant. α et β sont deux paramètres qui contrôlent l’importance relative entre phéromones et visibilité. Ainsi si α est égal à 0, le choix se fera uniquement en fonction de la visibilité (si β est différent de zero).
Mise à jour des phéromones
A la fin de chaque cycle (chaque fourmi a parcouru les n sommets qui composent le graphe), les variables des phéromones sont mises à jour selon la formule :
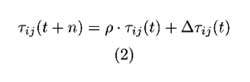
où ρ∈[0,1[ est un coefficient qui définira la vitesse d’évaporation des phéromones sur les arcs entre l’instant t et l’instant t+n, et où ∆τ (t) représente la quantité de phéromone déposée par les fourmis dans ce même intervalle de temps sur l’arc (i,j).
Le choix de ρ est important, en effet si ρ se rapproche trop de 1, on observe un effet de stagnation des phéromones sur les arcs, ce qui implique des inconvénients tel que le fait de voir les mauvaises solutions persister.
De même, choisir ρ≈ 0 implique une évaporation trop rapide des phéromones, donc amène la fourmi à un choix dépendant uniquement de la visibilité des nœuds.
Quantités de phéromones déposées
Appelons Tk(t) = (uk1,…,ukq) le tour réalisé par la k-ème fourmi dans l’intervalle de temps [t,t+,n], et Lk(t) sa longueur. Tk(t) (et donc Lk(t)) s’obtient en analysant la mémoire de la fourmi.
Soit ∆τijk (t), la quantité de phéromones déposée par cette fourmi sur l’arc (i,j) dans ce même intervalle de temps. On le définit ainsi :
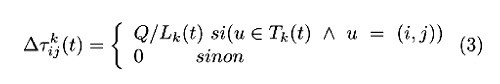
Où Q est une constante. On voit bien ici que les phéromones sont régulés en fonction de la qualité de la solution obtenue car plus Lk(t) est faible plus l’arc sera mis à jour en phéromones.
On peut maintenant définir le ∆τ (t) de la formule de mise à jour de phéromones ainsi :
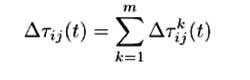
VI.3. Fonctionnement de l’algorithme :
Nous allons maintenant préciser les différentes étapes de l’algorithme au cours du temps.
Initialisation de l’algorithme. Les éléments s’agencent de la manière suivante au début de l’algorithme :
- 1. les M fourmis sont répartir aléatoirement sur les N villes.
- 2. Pour chaque fourmi, la liste qui modélise sa mémoire contient sa ville de départ.
- 3. Les pistes de phéromones sont initialisées comme suit : tij(0) = c, où c est une petite constante positive, qui ne peut être nulle (sinon, il y a un problème lors du calcul de (1))
Fin d’un cycle. Après n itérations, nous sommes à l’instant T, toutes les fourmis ont terminé leur tour, chacune a une liste «mémoire» pleine et est revenue à sa propre ville de départ. À ce moment :
- 1. Chaque fourmi calcule sa valeur Lk(t) .
- 2. Les variables τk (t) sont calculées conformément à la formule (1).
- 3. Les variables de phéromone τij(t) sont mises à jour suivant la formule(2).En d’autres termes, la fourmi refait son tour en sens inverse tout en déposant des phéromones.
- 4. On observe quelle fourmi a trouvé le tour de longueur minimum (i.e. on recherche la fourmi k telle que k = minm k=1Lk(t)). Si ce tour est meilleur que le meilleur tour jusqu’ici, on le mémorise.
- 5. Les mémoires des fourmis (liste des villes visitées) sont effacées.
- 6. Les fourmis recommencent un nouveau tour, toujours au départ de la ville sur laquelle elles avaient été placées au début de l’algorithme.
Fin de l’algorithme. On arrête l’algorithme après un nombre de cycles égal à une constante NC max. Si à partir d’un instant, toutes les fourmis font le même tour, l’algorithme s’interrompt :
On est dans une situation de stagnation où le programme arrête de chercher des alternatives. L’algorithme donne en retour le meilleur tour mémorisé.
Les paramètres permettant de caractériser complètement une instance de AS sont repris dans les tuplets : <m, p, α, β, Q, NCmax > , où 0≤p <1,α ≥0, β ≥0 et c >0.
VII. L’algorithme BicriterionAnt :
L’algorithme BicriterionAnt a été proposé par Iredi et al. [17] spécialement pour résoudre le problème de tournée de véhicules bi-critère. Pour ce faire, il utilise deux structures de traces de phéromone différentes, t et t’, une pour chaque critère considéré.
A chaque génération, problème. Durant l’étape de chacune des m fourmis de la colonie génère une solution au construction, la fourmi choisit le prochain sommet j à visiter relativement à la probabilité suivante :
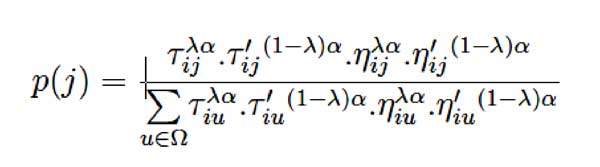
Où ᶯij et ᶯ’ij sont les valeurs heuristiques associées à l’arête a ij relativement au premier et second objectif, respectivement, Ω est le voisinage faisable de la fourmi, et est calculé pour chaque fourmi h, f 1, …, m, comme suit :
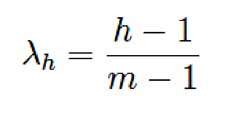
Une fois que toutes les fourmis ont construit leurs solutions, les traces de phéromone sont évaporées par la règle habituelle. Ensuite, chaque fourmi qui a généré une solution dans le front Pareto au cycle courant est autorisée à mettre à jour les deux structures phéromone t et t’, en déposant une quantité égale à 1/l, où l est le nombre de fourmis qui sont en train de mettre à jour les traces de phéromone. Les solutions non-dominées générées tout au long de l’exécution de l’algorithme sont mises dans un ensemble externe.
VIII. Algorithme proposé pour bi-objectifs:
VIII.1. Les formules :
On a comme donnée un fichier qui contient les cordonnées des villes, a partir de se fichier on calcule la matrice de distance D par la formule :
![]()
1 Est le poids de premier objectif qui est la distance.
La matrice de temps T est calculé par la formule :
![]()
La vitesse est constante. 2 Est le poids de deuxième objectif qui est la distance.
Avec ![]()
La matrice de décision M est calculé par la formule :
![]()
Après l’obtention de la matrice de décision M on applique l’algorithme Ant System de mono objectif.
IX. Conclusion :
Les nouvelles techniques d’intelligence artificielle peuvent être utiles quand de tels problèmes ne sont pas clairement et mathématiquement définis. Dans cette étude on utilisé l’algorithme à colonies de fourmis pour résoudre le problème de voyageur de commerce bi- objectifs.
Ce modèle d’algorithme est plus proche encore de la nature. Cette approche s’est révélée adéquate puisque les résultats sont très satisfaisants.
La Résolution du Problème de Voyageurs de Commerce Bi-Objectifs par La Métaheuristique d’Optimisation par Colonie de Fourmis Artificielles
Présenté pour l’obtention du diplôme de MASTER Option Réseaux et Multimédia
Département de Mathématique et d’Informatique