Application, Modélisation ARCH des rentabilités boursières de l’indice bancaire – Chapitre III :
Section 1- Les processus à non linéarités en variance : les modèle ARCH
Engel (1982) a développé les modèles ARCH afin de permettre à la variance d’une série de dépendre de l’ensemble d’informations disponible, et notamment du temps. Cette classe des modèles à pour objet de pallier les insuffisances des représentations ARMA traditionnelles non adaptés aux problématiques financiers. Les séries financières sont en effet caractérisées par une volatilité variable et par des phénomènes d’asymétrie qui ne peuvent être pris en compte par les modélisations de type ARMA. Or, il est particulièrement important de comprendre et de modéliser la volatilité d’une série. En effet, les décisions d’investissement dépendent fortement, non seulement de l’évaluation des rentabilités futures, mais également des risques afférents aux diverses actions constituant les portefeuilles. L’estimation de la volatilité de la rentabilité d’une action fournit une mesure du risque qui y est attaché. En outre, si le processus suivi par la volatilité est correctement spécifié, celui-ci peut fournir des informations utiles à la détermination du processus générant les rentabilités. Les modèles ARCH sont basés sur une paramétrisation endogène de la variance conditionnelle. Ces processus ont connus un succès important dans les applications financières. En raison du fait qu’ils permettent de réécrire le modèle structurel concernant les choix de portefeuille optimaux, les liens entre rentabilité d’actifs et la rentabilité du portefeuille de marché. Ces modèles ont fait l’objet des nombreuses extensions que nous nous proposons d’étudier ci après.
1.1- formulation générale
Dans le modèle de type ARCH, εt est un processus tel que : E(εt – εt-1) = 0
V(εt – εt-1) = σ2
Où σ2t représente la variance conditionnelle du processus εt. On voit que la variance peut varier au cours du temps dans ce type de processus, à la différence des processus ARMA où elle est supposé constante. D’après 1, le processus standardisé :
Zt = εt(σ2t)-1/2 = εt /σt 2
Est un processus dont l’espérance conditionnelle set nulle et dont la variance conditionnelle est constante et égale a l’unité. En générale le processus εt, n’est pas observable, il peut correspondre à l’innovation d’un processus du type ARMA ajusté sur la série étudiée Yt :
Φ(L)Yt = (L) εt 3
Ou encore à celle d’un processus général du type :
Yt = f (Xt-1 ;b)+ εt 4
Où f est une fonction des variables explicatives Xt-1 et d’un vecteur de paramètre b inconnus.
L’équation générant la série Yt est appelée équation de la moyenne, et reste très générale.
1.2- Processus ARCH et GARCH
Le processus ARCH (q) est le modèle de base des processus ARCH proposé par Engel (1982). Le modèle ARCH (q) est basé sur un paramétrisation quadratique de la variance conditionnelle σ2t apparaît comme une fonction linéaire des q valeur passés du processus du carrés des innovations.
Définition 1 : un processus ARCH (q) est donné par :
σ2t = α0 + Σ αi ε2t-i = α0 + α (L) ε2t 5
Où α0 > 0 et αi >= 0
Les contraintes sur les coefficients garantissent la positivité de la variance conditionnelle. On peut de plus montrer que cette variance est finie si Σ αi < 1. Le modèle ARCH (q) permet de prendre en compte les regroupements de volatilité, c’est-à-dire le fait que les fortes (faible) variations de prix sont suivies par d’autre fortes (faible) variations de prix mais dont le signe n’est pas prévisible. Bollerslev (1986) a généralisé le modèle initiale d’Engel en établissement le modèle GARCH (p,q). Cette extension consiste en introduction de valeur retardée de la variance dans son équation et est similaire à l’extension des processus AR aux ARMA. Cela permet une description plus parcimonieuse de la structure des retardes.
Définition 2 : un processus GARCH (p,q) est défini par :
Où α0 > 0 et αi >= 0 et β >= 0.
A nouveau, les contraintes sur les coefficients assurent la positivité de la variance conditionnelle1.
Bien entendu, lorsque p=0, le processus GARCH (p,q) se réduit au processus ARCH (q).
Posons en effet : Ut = ε2t – σ2t 7
Remplaçons σ2t par (ε2t – ut) dans l’équation 6 :
D’où
ε2t – ut = α0 + α (L) ε2t + β(L) [ε2t – ut] 8
[I – α (L) – β(L)] ε2t = α0 + [I- β(L)]ut 9
Ainsi, l’équation 9 s’interprète comme un modèle ARMA (max (p,q),p) sue la série des carrés des résidus. Cette nouvelle écriture permet d’écriture facilement les conditions de stationnarité faible. Celles-ci reposent sue l’existence d’une variance V(εt) = E(σ2t) indépendante du temps asymptotique.
Propriété 1 : une condition nécessaire et suffisante de stationnarité du processus GARCH (p,q) s’écrit : α(1) + β(1) = Σ αi Σ βj < 1 10
On traduit ici simplement le fait que si les racines du polynôme :
1 – Σ (αi + βj) Li 11
Sont à l’extérieur du disque unité, alors la séries E(ε2t) converge et le processus devient asymptotiquement stationnaire à l’ordre deux.
Remarque : Empiriquement, l’identification des ordres p et q d’un processus GARCH
s’effectue à partir de l’étude des autocorrélations partielles de la série ε2t. Ainsi, pour un processus ARCH (q), la fonction d’autocorrélation partielle s’annule à partir du rang q+1.
1 Nelson et Cao (1991) ont montré que ces conditions n’étaient pas nécessaires.
Pour un processus GARCH (p,q), cette fonction n’est pas en général pas nulle et décroît de façon exponentielle lorsque le nombre de retards augments1.
Les applications des modèles ARCH (q) et GARCH (p,q) en finance sont très nombreuses. Toutefois, selon certains auteurs, les formulations sont trop restrictives car elles imposent une relation quadratique entre l’erreur et la variance conditionnelle. Selon Nelson (1991), les modèles GARCH peuvent se révéler insuffisants pour deux raisons principales :
– Le choix d’une forme quadratique pour la variance conditionnelle a des conséquences importantes sur la trajectoire temporelle de la série. Typiquement, les séries sont caractérisées par des périodes de forte volatilité et faible volatilité. Au travers des modèles ARCH, l’impact des valeurs passées de l’innovation sur la volatilité présente est donc pris en compte en fonction de leur ampleur. Dans le cas des séries financières, la volatilité tend à être plus importante après baisse qu’une hausse. En d’autre terme, la volatilité tend à croître en réponse aux mauvaise nouvelles et à décroître en réponse aux bonnes nouvelles. Le choix d’une forme symétrique pour la variance conditionnelle ne permet pas de modéliser ce phénomène d’asymétrie.
– Une autre restriction des modèles ARCH traditionnels provient des contraintes de non négativité imposée sur le paramètre. Les modèles GARCH restent fortement contraints à ce que la variance conditionnelle soit positive. Par conséquence, un choc à toujours un effet positive sur la volatilité courante.
Ces critiques ont donné lieu au développement de trois processus : le modèle EGARCH (exponentiel), TGARCH (Threshold), QGARCH (quadratic).
1.3- une caractérisation générale des processus de type GARCH
Hentschel (1994) a montré qu’une grande nombre de processus de type GARCH (avec p=q=1) pouvaient être considérés comme des cas particuliers d’une transformation de BOX-COX appliquée à un modèle AGARCH (Absolu GARCH) :
![]()
1 Sandrine Lardic, économétrie des séries temporelles macro et financières, economeca, 2002, page 292
Où f v(εt) = |εt –b| – c(εt –b) pour λ>1, la transformation de Box-Cox est convexe, pour λ
– Pour λ = v = 1 et |c| <= 1, l’équation définit le processus AGARCH.
– Pour λ = b = 0 et v = 1 on retrouve le processus EGARCH
– Pour λ = v = 1, b=0 et |c| <= 1 on retrouve le processus TGARCH
– Pour λ = v = 2 et b=c=0, la relation se réduit à la définition d’un processus GARCH usuel.
– Pour λ = v = 2 et c=0, on obtient le processus GARCH asymétrique non linéaire introduit par Engel et Ng (1993).
– Le modèle ARCH non linéaire NARCH introduit par Higgins et Bera (1992) est donné par λ = v et b=c=0.
Remarque : le processus EGARCH n’apparaît pas comme un cas particulier de 121.
1.4- Rappel sur le test ARCH
Rappelons que le test ARCH a été introduit par Engel (1982). Supposons que l’équation de la moyenne soit décrite par un processus ARMA. On considère la série Yt générée par le processus suivant :
Φ(L)Yt = (L)εt
σ2t =α0 +Σαi ε2t 13
L’hypothèse nulle testée est celle d’homoscédasticité : α1…………….. αq= 0contre l’hypothèse alternative d’hétéroscédasticité conditionnelle, au moins un coefficient est différent de 0. Si l’hypothèse nulle est acceptée, alors σ2t =α0 : la variance conditionnelle est constante. En revanche si l’hypothèse nulle est rejetée, les résidus suivent un processus ARCH (q).
La mise en œuvre du test est simple et peut s’effectuer en trois étapes :
1- on estime l’équation de la moyenne, on récupère les résidus estimés εˆ et l’on calcule la série des εˆ2t.
2- on régresse εˆ2t sur une constante et sur ses q valeurs passés.
3- On calcule statistique TR2 où T est le nombre d’observations et R2 est le coefficient de détermination associé a la régression de l’étape 2.
Sous l’hypothèse nulle d’homoscédasticité, la statistique TR2 suit une loi de Khi Deux à q degrés de liberté. La règle de décision est :
– Si TR2 < X2(q), l’hypothèse nulle est accepté : il n’existe pas d’effet ARCH.
– Si TR2 >= X2(q), on rejette l’hypothèse nulle en faveur de l’hypothèse alternative d’hétéroscédasticité conditionnelle.
1.5- un bref aperçu des méthodes d’estimation
Les techniques usuelles d’estimation s’appliquent aux modèles ARCH sont les maximum de vraisemblance et des moindres carrés en deux étapes sont les plus utilisées1.
1.5.1- Le maximum de vraisemblance
La plupart des aléas relatifs aux séries financières ne suivent pas une loi normale. Toutefois, la densité gaussienne peut être utilisée pour calculer l’estimateur même si la vraie distribution n’est pas normale. On utilise alors la méthode du maximum de vraisemblance. Des conditions suffisantes de régularité permettant d’obtenir des propriétés de convergence et de normalité asymptotique ont été établies par Weiss (1982) dans le cas de modèle ARCH linéaire. La plus contraignante entre elles, est une condition d’existence du moment d’ordre 4 pour les résidus εt. Lumsdaine (1990) montre qu’il est possible de s’affranchir de cette contrainte dans le cas du modèle GARCH (1,1) et que les estimateurs du maximum de vraisemblance des différents paramètres sont convergents et asymptotiquement normaux.
Il est important de noter que, lorsque la vraie densité conditionnelle est normale, les estimateurs de la moyenne et de la variance sont asymptotiquement non corrélés. Ils peuvent ainsi être estimés séparément sans perte d’efficacité. Cette propriété ne tient plus en dehors de la classe de modèles ARCH traditionnels.
1 Pour plus de détails sur l’estimation des modèles ARCH, voir Gouriéroux (1992) et bollerslev, Engel et Nelson (1994)
Considérons un modèle GARCH (p,q) défini comme :
On pose
Yt = f (Xt ,b) + εt
σ2t = ht = α0 + α1ε2t-1 +….. + αqε2t-q + β1 σ2t-1 + …..+ βp σ2
Z’ = (1, ε2t-1….,ε2t-q, ht-1, …, ht-p) W’= (α0, α1…., αq , β1……, βp)
Soit θ Є où θ = (b’, w’) et est un sous ensemble compact d’un espace euclidien tel que εt a des moments d’ordre deux finis.
Désignons par θ0 la vraie valeur des paramètres.
On peut réécrire l’équation de la variance conditionnelle comme suite : ht = Z’tw 14
La log vraisemblance, pour un échantillon de T observations, s’écrit1
LT (θ) = 1/T Σlt(θ) 15
Où
lt(θ) = -1/2 log ht- [1/2 . ε2t/ ht] 16
La maximisation de la log vraisemblance par rapport aux paramètres α, β et b nous permet d’écrire les conditions du premier ordre :
δlt / δw = 1/2ht . δht / δw (ε2t/ht – 1)
δlt / δb = εtXt / ht + ½ ht δht / δb (ε2t/ht – 1)
Pour les modèles ARCH et GARCH, l’estimateur est obtenu en résolvant les équations du premier ordre. La résolution numérique peut être menée en utilisant différents algorithmes, dont l’algorithme BHHH (Berndt, Hall, Hall et Hausman (1974)). Pour le modèle ARCH (q) la méthode du score peut être appliquer relativement facilement, mais pour les modèle GARCH (p,q) les termes récursifs compliquent cette procédure. Ce pourquoi on préfère en générale utiliser l’algorithme BHHH décrit ci-après.
1 On a ici négligé la constante, cette dernière n’intervenant pas dans la procédure de maximisation
Soit θ(i) le vecteur des paramètres estimés après la iième interaction. θ(i+1) est donné par :
θ(i+1) = θ(i) + λi (Σ δlt/δθ . δlt/δθ’)-1 Σ δlt/δθ 16
Où δlt/δθ est évalué en θ(i), λi est un multiplicateur.
Weiss (1982) a montré que l’estimateur du maximum de vraisemblance θˆT est un estimateur fortement convergent de θ0 et asymptotiquement normal de moyenne θ0 et de matrice de variance covariance dépendant de la loi conditionnelles de εt Soit :
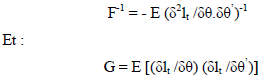
Si la vraie distribution conditionnelle de εt est normal, c’est-à-dire si : εt εt -1 ˜ N(0,ht), alors G=F et la matrice de variance covariance est donnée par : F-1GF-1 = F-1
Si l’on relache l’hypothèse de normalité et si l’on suppose simplement que :
E (εt εt -1) = 0
V(εt εt -1) = ht
E(ε4t εt -1) = h2t < infini
Alors θˆT est un estimateur asymptotiquement normal de θ0 de moyenne θ0 et de matrice de variance covariance F-1GF-1.
1.5.2- Les moindres carrés en deux étapes
Un modèle ARCH peut être vu comme deux modèles ARMA successifs, l’un sur le processus lui-même, le seconde sur le carrés des innovations. Il est de ce fait naturel d’introduire des procédures d’estimation en deux étapes tenant compte de cette structure particulière.
Soit un modèle de régression avec erreurs ARCH :
Yt = f (Xt, b) + εt
V = ht = α0 + α1ε2t-1 +….. + αqε2t-q 17
La première étape à obtenir des estimateurs convergents des paramètres de l’équation de la moyenne et de l’équation de la variance. L’estimateur de b est obtenu naturellement par l’estimation MCO déduite de la régression de Yt sur f (Xt, b). Notons cet estimateur bˆ. les résidus estimés sont alors donnés par :
εt = Yt – Xtbˆ 18
En régressant εˆ2t sur 1, εˆ2t-1…. εˆ2t-q, on obtient des estimateurs convergents des paramètres figurant dans l’équation de la variance :
Ces deux régressions successives ont été effectuées par la méthode des moindres carrés ordinaires, c’est-à-dire sans prendre en compte le phénomène d’hétéroscédasticité. Les estimateurs de b peuvent être améliorés dans la seconde étape en régressant Yt sur f (Xt, b) par le moindres carrés quasi généralisés avec : hˆt = σˆ2t = αˆ0 + αˆ1εˆ2t-1 +….. + αˆqεˆ2t-q 19
On note ces estimateurs de la seconde étape bˆ.
Lorsque la vraie distribution est conditionnellement normale, on a : V(ε2t εt -1) = 2h2t
Et des estimateurs de la seconde étape obtenus en régressant εˆ2t sur εˆ2t-1 … εˆ2t-q. par le MCQG avec V(ε2t εt -1) = 2hˆ2t.
Asymptotiquement normaux, ces estimateurs de MCQG font apparaître une perte d’efficacité asymptotique par rapport à ceux du pseudo maximum de vraisemblance. Il est important de noter que celle-ci n’affecte que les paramètres de la moyenne : les estimateurs des paramètres de la variance sont asymptotiquement efficaces. Notons enfin que la méthode présentée ici peut s’appliquer à d’autres paramétrisations, notamment les modèles ARCH à seuils.
1.6- Modèles ARCH et prévision
La question de la prévision dans le cadre des processus de type ARCH a été abordée par de nombreux acteurs. Engel et Kraft (1983) ainsi que Engel et Bollerslev (1986) ont dérivé les expressions de la variance de l’erreur de prévision dans le cas de processus avec erreurs ARCH et GARCH respectivement. Bollerslev (1986) ainsi que Granger, White et Kametra (1989) se sont intéressés à la construction d’intervalles des confiances pour des prévisions à un pas. Dans la domaine des prévisions, on pourra également consulter les travaux de Geweke (1989) Baillie et Bollerslev (1992) ou encore Nelson et Foster (1994).
Considérons u processus GARCH (p,q) :
![]()
On peut écrire à l’horizon T :
σ2t+T = α0 + Σαiε2t+T-i + Σβjσ2
Soit encore :
![]()
Où n= min (m,T-1) et m = max(p,q)
En notant It ‘ensemble d’informations disponible à la date t, on a :
![]()
Car E[ε2t+T | It] = E[σ2t+T | It] si T > 0
A titre d’exemple, considérons un processus GARCH (1,1). On a naturellement p=q=1, donc m = 1, pour T>=2, n = min(1,T-1) = 1.
Par conséquent, on en déduit la relation suivante :
![]()
En notant E[σ2| It] = σˆ2t+T
on a donc la formule récursive suivante pour T>=2.
σˆ2t+T = α0 + (α1 + β1) σ2t+T-1 25
![]()
Bien évidemment, lorsque l’horizon de prévision T vaut 1, on a : ![]()
Les prévisions de la volatilité peuvent donc être effectuée selon l’équation 25 pour des horizon de prévisions supérieurs à un pas et selon 26 pour les prévisions statiques (prévisions à un pas1).
Ainsi, lorsque l’horizon de prévision augmente, la prévision optimale converge de façon monotone vers la variance non conditionnelle α0 / (1- α1 – β1).
1 On peut réécrire la relation 25 sous une forme alternative, valable quel que soit l’horizon, soit σˆ2t+T = α0 +ΣT-1 (αi + βi)i + (αi + βi)T-1 [αiε2t + β1σ2t ]
Lire le mémoire complet ==>
(La Bourse de Beyrouth : Test de l’efficience du marché financier)
Mémoire de fin d’année du Master 2 recherches APE « analyse et politique économique »
Université Montpellier 1

