7.3 Scénario d’application
Dans cette section, nous présentons le calcul du risque utilisant le modèle présenté pour une transaction de commerce électronique. Le scénario de l’application est celui que nous avons utilisé au chapitre 6. Il s’agit d’une transaction de commerce électronique; la transaction est paramétrée par le coût de la transaction (la somme totale engagée) et l’historique des entités participant à la transaction.
Dans cet exemple de transaction, la négociation est réalisée entre le client A et le vendeur B. Chaque partie utilise le risque comme paramètre de la transaction. Pour chaque partie, nous identifions d’abord le risque potentiel, puis nous en calculons la valeur en utilisant le modèle que nous venons de présenter. Notons que nous réutilisons la structure d’événements définie dans l’exemple d’application du chapitre 6.
7.3.1 Politique du tiers de paiement
Le client et le vendeur impliqués dans une transaction peut utiliser le service d’un tiers de paiement pour gérer le paiement. Nous supposons que le tiers de paiement T T P utilise pour sa politique par les contraintes suivantes :
-Le client peut déposer un montant pour un paiement d’une transaction, la commission dans ce cas est de 5% du montant de la transaction. Par contre, quand il a déposé le montant pour la transaction, et qu’il veut le récupérer, il doit payer une commission de 20% du montant.
-Le vendeur, pour récupérer le paiement d’une transaction, doit également payer une commission de 5% du montant de la transaction.
7.3.2 Client A
Lors de cette transaction, le client A peut avoir à prendre le risque de payer le vendeur et de ne pas recevoir l’objet commandé (perdre la somme d’argent et ne pas avoir le bien convoité). La perte de la somme d’argent, si elle survient, dépend du mode de paiement qui a été utilisé. Le risque que nous déterminons est le risque global pour tout le processus de la transaction. Ce risque est estimé en se basant sur le coût/bénéfice des conséquences possibles.
Le client considère que la transaction est réussie s’il reçoit le produit après l’avoir commandé. La transaction réussie est considérée un bénéfice. Nous pouvons quantifier ce bénéfice par un pourcentage du montant du produit. Nous fixons arbitrairement un pourcentage de bénéfice à 10% du montant en cas de transaction réussie.
On choisit de ne pas compter de coût/bénéfice au cas où le produit n’est pas obtenu à causedu fait du vendeur, et l’on ne quantifie pas la variation de réputation du client (bon payeur, mauvais payeur, etc on pourrait considérer qu’une bonne réputation est un bénéfice chiffrable). Pourtant, si le client ne reçoit pas le produit à cause de son comportement (il chosit de ne pas envoyer le paiement), l’on considère ce fait comme perte du client parce que le client a besoin du produit. Cette perte est fixée par une valeur à 10% du montant.
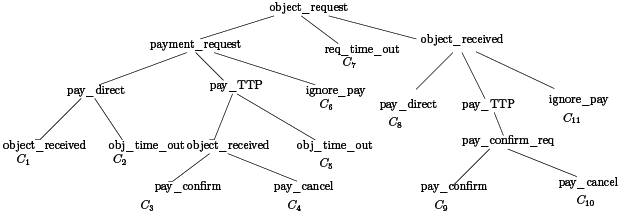
Pour le client, nous obtenons les conséquences possibles pour une transaction, spécifiées par l’arbre des probabilités illustré dans la figure 7.2
7.3.2.2 Spécification des conséquences
Grâce à l’arbre des probabilités, nous pouvons obtenir les conséquences suivantes qui peuvent donner un bénéfice ou causer une perte, concernant l’évaluation du risque. Les conséquences sont données en parcourant l’arbre des probabilités. Les gains et les pertes sont évaluées plus précisémennt à la section 7.3.2.4
-C1 : A reçoit une demande de paiement après avoir commandé le produit. Il paie directement le vendeur (pay_direct) et reçoit le produit. La perte financière est 0. La transaction est réussie, et le bénéfice est de 10% du montant de la transaction.
-C2 : A reçoit une demande de paiement après avoir commandé un produit. Il paie directement au vendeur et ne reçoit pas le produit. La perte financière est égale au montant engagé pour la transaction et le client ne dispose pas du produit.
Fig. 7.2 Arbre des probabilités du client
-C3 : A reçoit une demande de paiement après avoir commandé le produit. Il paie en utilisant les services d’un tiers de confiance (pay_T T P ) et reçoit le produit. Ensuite, il confirme le paiement (pay_conf irm). La perte financière est la commission de 5% payée au TTP, selon la politique du TTP, le client dispose du produit et le bénéfice est de 10% du montant.
-C4 : se déroule comme C3 , sauf à la fin où le client annule le paiement (pay_cancel).
Dans ce cas, selon la politique de TTP, il devra payer une commission de 20% du montant de la transaction pour une action de ce type. Il reçoit le produit et le bénéfice est donc de 10% du montant.
-C5 : A reçoit une demande de paiement après avoir commandé le produit. Il paie en utilisant les services d’un tiers de confiance et ne reçoit pas le produit. La perte financière se monte au montant de la commission (20%) que A verse au tiers de confiance pour obtenir le remboursement du montant de la transaction; A ne dispose pas du produit.
-C6 : le client reçoit une demande de paiement après avoir commandé un produit.
Il ne paie pas et le client ne dispose pas du produit. La perte dans ce cas est de 10% du montant.
-C7 : le client commande le produit, mais le vendeur ne valide pas sa commande.
La perte est 0.
-C8 : le client reçoit le produit après l’avoir commandé. Il reçoit ensuite la demande de paiement du vendeur et il le paie par une méthode direct. La perte financière dans ce cas est 0. Il dispose du produit et le bénéfice est donc 10% du montant.
-C9 : le client reçoit le produit après l’avoir commandé. Il reçoit ensuite la demande de paiement du vendeur et il le paie par une méthode utilisant un tiers sûr. Ensuite, il envoie la confirmation de paiement (pay_conf irm). Il doit payer une commission de 5% qui est considérée comme une perte. Il dispose du produit et un bénéfice de 10% du montant.
-C10 : se déroule comme C8 , sauf à la fin où le client annule le paiement (pay_cancel).
Il doit payer une commission de 20% pour récupérer le dépôt selon la politique du TTP. La perte financière dans ce cas est 20% du montant de transaction. Il dispose du produit.
-C11 : le client reçoit une demande de paiement après avoir commandé et reçu le produit. Il reçoit ensuite la demande de paiement de vendeur et il ne le paie pas.
Le client, comme pour C10 a fait un bénéfice illégal correspondant à la valeur du produit.
En calculant le coût/bénéfice en pratique, si c’est une perte, nous mettons une valeur négative pour la conséquence; si c’est un bénéfice, nous mettons une valeur positive. Soit P est le coût du produit, nous avons le tableau 7.1 indiquant le coût/bénéfice de l’ensemble de conséquences.
| Conséquence C1 | Avant transaction P | Après la transaction P*(1+10%) | Coût/Bénéfice 10% |
| C2 | P | 0 | -100% |
| C3 | P | P*(1-5%+10%) | 5% |
| C4 C5 C6 | P P P | P*(1+1-20%+10%) P*(1-20%) P*(1-10%) | 90% -20% -10% |
| C7 | P | P | 0% |
| C8 | P | P*(1+10%) | 10% |
| C9 | P | P*(1-5%+10%) | 5% |
| C10 | P | P*(1+1-20%+10%) | 90% |
| C11 | P | P*(1+1+10%) | 110% |
Tab. 7.1 Conséquences de transactions du client
7.3.2.3 Probabilité des conséquences
Nous devons maintenant déterminer la probabilité, le coût ou le bénéfice de chacune des conséquences potentielles pour évaluer le risque lié à la transaction. Pour la probabilité des conséquences, nous devons considérer deux situations :
1. le client A mène sa première transaction avec le vendeur B. L’historique H est donc limité à la session en cours. Dans ce cas, le client peut proposer un arbre des probabilités en accord avec sa perception. Supposons qu’il propose un arbre où soit associé aux branches qui mènent aux nœuds payement_request, req_time_out et object_received les probabilités 0.7, 0.1 et 0.2. Les autres branches de l’arbre sont équiprobables.
En appliquant l’algorithme de calcul des probabilités de dépendance ci-dessus, nous avons des probabilités de conséquences Ci( i = 1 . . . 11) qui sont respectivement : 0.7/6, 0.7/6, 0.7/12, 0.7/12, 0.7/6, 0.7/3, 0.1, 0.2/3, 0.2/6, 0.2/6, 0.2/3.
2. Le client A a déjà mené des transactions avec le vendeur B. Nous déterminons la probabilité d’occurence de chacune des conséquences en utilisant les informations disponibles dans l’historique. Il faut aussi souligner que le nombre de sessions de l’historique doit être suffisant pour un calcul efficace.
Nous appliquons l’algorithme de calcul des probabilités pour les conséquences indirectes et nous obtenons la probabilité de chaque conséquence finale abordée ci-dessous. Par exemple, pour calculer la probabilité de la conséquence C1 , nous pouvons réaliser les étapes suivantes :
-Compter le nombre de sessions de l’historique qui contiennent la chaîne des événements suivants dans cet ordre : {object_request, payment_request, pay_direct, object_received}, noté par nbC1 .
-La probabilité de cette conséquence sera nbC1 /nbS . Nous pouvons voir facilement que ce calcul correspond à l’algorithme de calcul des probabilités dépendantes donné ci-dessus.
Le calcul de la probabilité des autres conséquence est réalisé de la même manière. Supposons qu’au moment de la transaction A ait l’historique suivant :
H ={object_request, payment_request, pay_direct, low_risk, object_received}
{object_request, payment_request, pay_direct, low_risk, time_out}
{object_request, payment_request, pay_direct, low_risk, time_out}
{object_request, payment_request, pay_T T P, high_risk, object_received, pay_conf irm}
{object_request, payment_request, pay_T T P, low_risk, object_received, pay_cancel}
{object_request, payment_request, pay_T T P, high_risk, time_out}
{object_request, object_received, pay_direct, high_risk}
En appliquant l’algorithme de calcul des probabilités, nous obtenons les probabilités pi de chaque conséquence Ci : p1 = 1/7, p2 = 2/7, p3 =1/7, p4=1/7, p5=1/7, p6 = p7 = 0, p8 = 1/7, p9 = p10 = p11 = 0.
7.3.2.4 Coût/bénéfice des conséquences
Maintenant, il nous faut déterminer le coût/bénéfice de chaque conséquence. Supposons que le montant de la transaction considérée soit 100 e et que la commission retenue en cas de remboursement par le tiers de confiance soit de 10%.
En appliquant les calculs du coût/bénéfice donnés dans le tableau 7.1, nous obtenons le coût/bénéfice des conséquences Ci (i = 1 . . . 11) qui sont respectivement : 10, -100, 5, 90, -20, -10, 0, 10, 5, 90, 110
7.3.2.5 Valeur du risque
En appliquant la formule du calcul de risque à cette transaction, nous obtenons la valeur du risque. Considérons aussi deux cas :
1. L’historique au moment de transaction est vide. Le résultat trouvé dans ce cas sera :
P p(oi ) ∗ cb(oi ) = 10 ∗ 0.7/6 − 100 ∗ 0.7/6 + 5 ∗ 0.7/12 + 90 ∗ 0.7/12 − 20 ∗ 0.7/6 − 10 ∗ 0.7/3 + 0 ∗ 0.1 + 10 ∗ 0.2/3 + 5 ∗ 0.2/6 + 90 ∗ 0.2/6 + 110 ∗ 0.2/3 = 1.5
2. L’historique au moment de transaction est celui donné ci-dessus, dans le risque est alors :
P p(oi ) ∗ cb(oi ) = 10 ∗ 1/7 − 100 ∗ 2/7 + 5 ∗ 1/7 + 90 ∗ 1/7 − 20 ∗ 1/7 − 10 ∗ 0 + 0 ∗ 0 + 10 ∗ .1/7 + 5 ∗ 0 + 90 ∗ 0 + 110 ∗ 0 = −15
7.3.3 Vendeur B
Pour limiter ses risques financiers, le vendeur n’envoie le produit au client que lorsqu’il en a reçu le paiement. Selon notre modélisation, un paiement valide est soit un paiement direct (payment_received), soit une confirmation de paiement de la part d’un tiers de confiance (pay_T T P _notif ied).
Lors d’un paiement direct, le vendeur ne prend aucun risque : il peut vérifier que le paiement a été réalisé (que le montant correspondant à la transaction lui a été crédité) avant d’envoyer le produit.
Dans la deuxième situation, il est possible que le vendeur ne reçoive pas le paiement dans les situations suivantes : le client ne confirme pas la livraison de sa commande auprès du tiers de confiance; le tiers de confiance est défaillant et n’effectue pas le paiement.
Le risque considéré est aussi global, basé sur le coût/bénéfice des conséquences possibles, en comptant également la commission payée pour le tiers de paiement et le bénéfice en cas d’une transaction réussie (transaction pour laquelle, le vendeur reçoit un paiement valide). Nous fixons aussi ce bénéfice à 10% du montant de la transaction.
Comme dans le cas du client, on considère qu’une vente qui échoue n’entraîne ni gain ni perte, et l’on ne tient pas compte des implications liées à la réputation du vendeur.
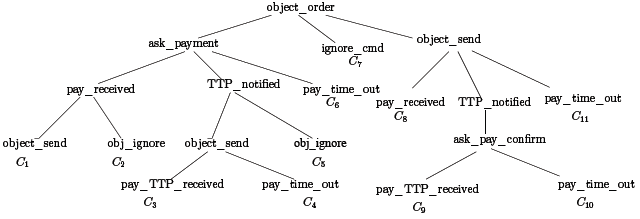
L’arbre des probabilités qui modélise ces conséquences possibles d’une transaction du vendeur est illustré dans la figure 7.3
Fig. 7.3 Arbre des probabilités du vendeur
7.3.3.2 Spécification des conséquences
Nous pouvons trouver les différentes conséquences de la transaction en parcourant l’arbre des probabilités des conséquences.
-C1 : B reçoit une commande (object_order ) et il demande un paiement au client.
Il envoie le produit au client A après avoir reçu le paiement (payment_received); la perte financière potentielle est nulle et le produit est envoyé. Le bénéfice est 10% du montant.
-C2 : B reçoit une commande (object_order ) et il demande un paiement au client. Il n’envoie pas le produit au client A après avoir reçu le paiement (payment_received); dans ce cas, il fait un bénéfice illégal qui a pour valeur le montant de la transaction et le produit n’est pas envoyé. Il compte aussi le bénéfice de 10% lié à la réception du paiement.
-C3 : B reçoit une commande (object_order ) et il demande un paiement au client.
Il envoie le produit au client A après avoir reçu la notification du paiement (payment_T T P _notif ied). Au final, il reçoit la confirmation du paiement par le tiers (payment_T T P _received). La perte financière est de 5% de la valeur du produit pour récupérer le paiement, selon la politique du TTP. La transaction réussit et il a aussi un bénéfice de 10% du montant. Le produit est envoyé.
-C4 : B reçoit une commande (object_order ) et il demande un paiement au client.
Il envoie le produit au client A après avoir reçu la notification du paiement (payment_T T P _notif ied); Au final, il ne reçoit jamais la confirmation de paiement par le tiers (payment_tim_out). La perte dans ce cas est le montant de la transaction.
-C5 : B reçoit une commande (object_order ) et il demande un paiement au client.
Il décide ensuite qu’il ne veut plus réaliser la transaction et l’annule donc (ignore ). Le coût dans ce cas est 0.
-C6 : B reçoit une commande (object_order ) et il demande un paiement au client, le client ignore la transaction. La perte dans ce cas est 0.
-C7 : B reçoit une commande (object_order ) mais il ignore cette commande ignore_cmd.
Le coût est égal à 0.
-C8 : B envoie le produit au client après avoir reçu une commande (object_order ).
Ensuite il demande un paiement et finalement reçoit un paiement direct valide (payment_received ). La perte dans ce cas est 0. La transaction est réussie et il a donc fait un bénéfice de 10% du montant.
-C9 : B envoie le produit au client après avoir reçu une commande (object_order ).
Ensuite il demande un paiement et finalement reçoit la notification du paiement par le tiers, payment_TTP_notified, ensuite une confirmation de paiement (payment_received ). La perte financière dans ce cas est 5% du montant de transaction selon la politique du TTP. Le bénéfice est 10% pour ce cas de transaction réussie.
-C10 : comme C8 sauf au final, le vendeur n’a pas la confirmation de paiement (payment_TTP_time-out ). La perte dans ce cas est le montant de la transaction.
-C11 : B envoie le produit au client après avoir reçu une commande (object_order ).
Ensuite il demande un paiement, mais il ne le reçoit jamais (payment_time-out ). La perte est égale à la valeur de l’objet.
Soit P le coût du produit, nous avons le tableau 7.2 indiquant le coût/bénéfice de l’ensemble de conséquences.
7.3.3.3 Probabilités des conséquences
Pour déterminer la probabilité de chaque conséquence, nous devons également considérer deux cas : au moment de la transaction, le vendeur fait la première transaction avec le client ou la nieme transaction.
1. le vendeur B en est à sa première transaction avec A. Dans ce cas, l’historique H de B est vide. Comme dans le cas du client, le vendeur peut proposer un arbre des probabilités selon sa perception pour les premières transactions. Supposons qu’il propose l’arbre, où les probabilités des branches de la racine ask_payement, ignore_cmd et object_send sont respectivement 0.8, 0.1 et 0.1. Les autres branches de l’arbre sont équiprobables. En appliquant l’algorithme de calcul des probabilités de dépendance ci-dessus, nous obtenons les probabilités des conséquences
| Conséquence C1 | Avant transaction P | Après la transaction P*(1+10%) | Coût/Bénéfice 10% |
| C2 | P | P(1+1+10%) | 110% |
| C3 C4 C5 | P P P | P*(1-5%+10%) P | 5% -100% 0% |
| C6 | P | P | 0% |
| C7 | P | P | 0% |
| C8 | P | P*(1+10%) | 10% |
| C9 C10 | P P | P(1-5%+10%) 0 | 5% -100% |
| C11 | P | 0 | -100% |
Tab. 7.2 Conséquences de transactions du vendeur
C1, C2 , C3 , C4, C5 , C6 , C7 , C8 , C9 , C10 et C11 qui sont respectivement : 0.8/6, 0.8/6,0.8/12, 0.8/12, 0.8/8, 0.8/3, 0.1, 0.1/3, 0.1/6, 0.1/6 et 0.1/3.
2. le vendeur B a déjà effectué des transactions avec A. Dans ce cas, la probabilité des conséquences Ci sera déterminée en utilisant les informations disponibles de l’historique des transactions.
De la même façon, nous appliquons l’algorithme de calcul des probabilités pour les conséquences indirectes. Pour calculer la probabilité de la conséquence C1, nous pouvons réaliser les étapes suivantes :
-Compter le nombre de sessions de l’historique qui contiennent la chaîne des événements suivante : {object_order, ask_payment, payment_received, object_send}, noté par nbC1 .
-La probabilité de cette conséquence sera nbC1 /nbS .
La probabilité des autres conséquence sera calculée de la même manière. Supposons qu’au moment de la transaction B, ait l’historique suivant :
HS ={object_order, ask_payment, pay_received, object_send . . . }
{object_order, ask_payment, pay_T T P _notif ied, ignore . . . }
{object_order, ask_payment, pay_T T P _notif ied, object_send, payment_received . . . }
{object_order, ask_payment, pay_T T P _notif ied, object_send, payment_received . . . }
{object_order, ask_payment, pay_T T P _notif ied, object_send, payment_time_out . . .
{object_order, object_send, ask_payment, payment_received . . . }
{object_order, object_send, ask_payment, payment_time − out . . . }
En appliquant l’algorithme de calcul de la probabilité des conséquences, nous obtenons la probabilité pi de chaque conséquence Ci : p1 =1/7, p2=0, p3 =2/7, p4=1/7,p5=1/7, p6=0, p7=0, p8=1/7, p9 = p10 = 0, p11 =1/7.
7.3.3.4 Coût/bénéfice
Supposons que le montant de la transaction considérée soit 100 e. Nous pouvons estimer le coût/bénéfice de chaque conséquence en utilisant le tableau de calcul coût/bénéfice 7.2. Nous obtenons le coût/bénéfice des conséquences Ci (i = 1 . . . 11) qui sont respectivement : 10, 110, 5, -100, 0, 0, 0, 10, 5, -100, -100.
7.3.3.5 Évaluation
La valeur du risque est évaluée avec la probabilité et le coût/bénéfice de chaque conséquence estimée, en utilisant la formule de la fonction PDF. Considérons deux cas :
(a) L’historique au moment de la transaction est vide. Le résultat trouvé dans ce cas sera :
P p(oi ) ∗ cb(oi ) = 10 ∗ 0.8/6 + 110 ∗ 0.8/6 + 5 ∗ 0.8/12 − 100 ∗ 0.8/12 + 0 ∗0.8/8 + 0 ∗ 0.8/3 + 0 ∗ 0.1 + 10 ∗ 0.1/3 + 5 ∗ 0.1/6 − 100 ∗ 0.1/6 − 100 ∗ 0.1/3 = 5.1
(b) L’historique au moment de transaction est celui donné ci-dessous, dans ce cas le risque est :
P p(oi ) ∗ cb(oi ) = 10 ∗ 1/7 + 110 ∗ 0 + 5 ∗ 2/7 − 100 ∗ 1/7 + 0 ∗ 1/7 + 0 ∗ 0 + 0 ∗ 0 + 10 ∗ 1/7 + 5 ∗ 0 − 100 ∗ 0 − 100 ∗ 1/7 = −24
7.3.4 Échantillonnage du risque
Nous venons de voir de quelle manière peut être calculée la valeur du risque pris par chacune des parties engagées dans une transaction. Il est nécessaire de ré-échantilloner ces niveaux de risque pour pouvoir les traduire en événements : low_risk, medium_risk, high_risk.
Les seuils pour l’échantillonnage peuvent être calculés après le processus d’apprentissage par les essais. Le bénéfice est une valeur positive, et le coût porte une valeur négative dans ce cas. Dans le cadre du sénario proposé en exemple, après quelques essais d’apprentissage de chaque côté, le client et le vendeur, les échelles suivantes peuvent être appliquées :
-Pour le client, nous distinguons les niveaux :
-≥ 0 : low_risk
–10 à 0 : average_risk
-≤ -10 : high_risk
-Pour le vendeur, nous distinguons les niveaux :
-≥ 0 : low_risk
–15 à 0 average_risk
-≤ -15 : high_risk
7.3.5 Discussion
Quand nous identifions le risque de la transaction, nous nous intéressons aux risques importants qui concernent la réussite globale de la transaction, ceux que nous avons abordés ci-dessus. Pourtant, il y a aussi d’autres aspects également liés aux risques que nous ne prenons pas en compte, tels que :
- -Pour le client, il y a un risque que la qualité du produit ne soit pas conforme à celle qui était décrite.
- -Pour le vendeur, il y a un risque que le paiement du produit livré ait été fait avec un moyen de paiement volé ou falsifié (numéro de carte VISA volé).
- -Il y a aussi des risques liés au transport entre les deux parties, tels que par exemple la perte du produit, un retard de livraison. . .
- -Les coûts indirects liés à la baisse de réputation d’un client ou d’un vendeur, etc.
La prise en compte de ces aspects aurait alourdi l’exemple proposé, mais elle peut s’effectuer si l’on veut obtenir des modèles plus réalistes.
Nous pouvons constater facilement que la valeur du risque évolue après chaque transaction. Le fait que l’historique change après chaque transaction implique le changement de la probabilité des conséquences, et le risque évolue donc. C’est aussi un fait indiquant qu’il est nécessaire de réévaluer les probabilités quand on veut lancer une nouvelle transaction.
7.4 Synthèse
Nous avons présenté dans ce chapitre notre réalisation de la gestion du risque. Nous avons défini des phases dans la gestion du risque afin de concevoir ce module. Ensuite, un modèle du risque basé sur l’approche quantitive a été intégré à notre système de gestion de la confiance. Enfin, nous avons détaillé notre modèle en analysant le risque pour le scénario d’application d’une transaction du commerce electronique.
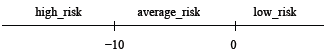
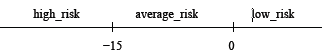

Merci beaucoup de m’avoir intégrer dans votre site