4.3. Construction d’un modèle de valorisation d’action sur base du mouvement brownien
4.3.1. Qu’est-ce que le mouvement brownien?
Le mouvement brownien a été décrit la première fois en 1827 par le botaniste écossais Robert Brown. La petite histoire nous dit qu’il étudiait le mouvement complètement aléatoire de minuscules grains de pollen plongés dans de l’eau emprisonnée dans un bloc de quartz. Au départ, les biologistes attribuaient ces mouvements à une «force vitale» qui était sensée être la source de la vie.
En fait, l’explication de ce phénomène est physique : le mouvement des grains est le résultat visible des chocs entre ces grains et les molécules d’eau. Les molécules d’eau étant en agitation constante, celles-ci entrent en collision avec les grains de pollen et la résultante de ces nombreuses collisions produit le déplacement de ces grains dans le liquide. Ces mouvements sont d’amplitude et de direction complètement aléatoire. Le graphe suivant illustre la trajectoire que peut prendre un de ces grains.
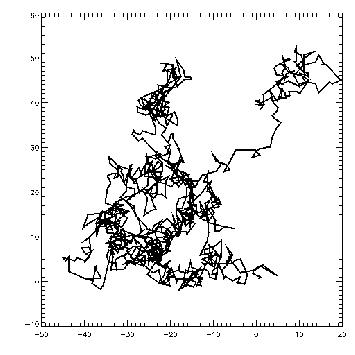
(Source : Wikipedia, URL : http://fr.wikipedia.org/wiki/Bruit_thermique, page consultée le 22/07/08)
4.3.2. Caractéristiques du mouvement brownien.
Un mouvement brownien est caractérisé par un déplacement statistiquement nul, et ces mouvements suivent une distribution de probabilité dont la variance est fonction de l’énergie contenue dans le liquide (c’est à dire sa température) et de la viscosité du liquide. Donc, plus le liquide est chaud, plus les mouvements de la particule ont une grande amplitude. Et plus le liquide est visqueux, moins les mouvements sont importants.
La deuxième caractéristique provient du fait que nous supposons que le mouvement brownien est soumis à une distribution de probabilité. Ceci implique que chaque mouvement est indépendant de ceux qui ont précédés et de ceux qui suivront. Ceci implique donc que le mouvement brownien n’a aucune «mémoire» de ses déplacements.
Le graphe précédent illustre un mouvement tel qu’il a pu être observé à l’intérieur d’un liquide. Ce graphe est en deux dimensions, ce qui signifie que le mouvement observé a deux degrés de liberté : un selon l’axe des x et l’autre selon l’axe des y. Imaginons maintenant un mouvement brownien à un seul de degré de liberté, c’est à dire un point se déplaçant aléatoirement le long d’une droite. On pourrait représenter un graphe où les mouvements sont enregistrés périodiquement, donc à chaque valeur de temps t correspond un déplacement. Ce qui nous donnerait par exemple, le graphe suivant :
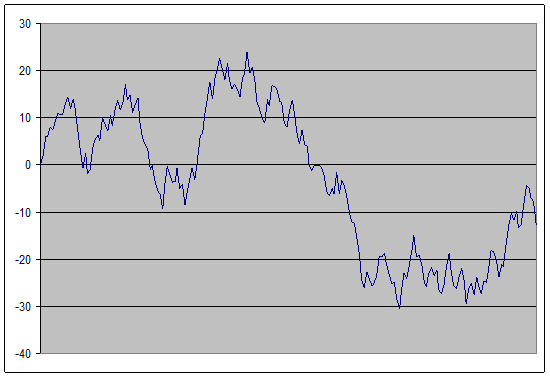
On remarque assez vite la similitude avec un graphe de cours d’action. Nous allons donc tenter de voir si il est possible de modéliser le cours d’un instrument financier en utilisant le mouvement brownien. Pour ce faire nous allons d’abord vérifier que les cours boursiers et les mouvements browniens ont les mêmes caractéristiques.
4.3.3. Comparaison des données réelles avec les caractéristiques du mouvement brownien.
Pour vérifier si les cours des actions ont un comportement semblable au mouvement brownien nous allons prendre le cours de plusieurs actions et voir si ces cours sont distribués selon une loi de probabilité et centrés en zéro et si ces cours arrivent aléatoirement, c’est à dire indépendamment des cours précédents. Nous allons donc choisir des actions cotées depuis assez longtemps pour pouvoir avoir un grand nombre de mesures et qui sont suffisamment liquides pour que les cours ne soient pas influencés par des pénuries de liquidités.
Selon Richard Dennis, un ancien gourou de la finance, il est possible sur base de l’analyse technique de spéculer sur n’importe quel marché sans même savoir sur quoi on traite. En effet, selon les trois principes généraux de l’analyse technique :
– le prix défini sur un marché prend absolument toutes les informations en compte.
– L’histoire est cyclique et les mêmes causes ont les mêmes effets.
– Il existe des tendances.
A la lumière des ces principes, il est donc intéressant d’utiliser directement les cours de bourse comme matière première de notre étude. En effet, en utilisant ces données, nous sommes certains d’intégrer toutes les informations disponibles au moment où les prix sont fixés par le marché. Nous allons aussi essayer de voir dans quelle mesure on peut dégager des tendances ou des cycles ou si les marchés sont réellement aléatoires.
Nous allons donc choisir d’utiliser des cours de clôture car ceux-ci sont calculés sur des intervalles de temps réguliers, ce qui n’est pas le cas des cours en intraday dont la période entre deux échanges peut varier considérablement. La stabilité des périodes de cotation des cours de clôture nous semblait mieux adaptée à la comparaison avec un mouvement brownien à 1 degré de liberté.
4.3.3.1. Choix des données
Nous avons choisi les valeurs cotées sur Euronext dans les indices BEL20 sur Bruxelles et CAC40 sur Paris. Les données utilisées que vous pourrez trouver en annexe ont été transmises par GL TRAD. Ces données ont été prises au 21/12/07 et représentent 213 943 cours différents. Voici la liste des valeurs étudiées :
– Pour le BEL20 :
| Nom | Symbole | à partir du | nb de cotations |
| Ackermans V.Haaren | ACKB | 24/04/2007 | 164 |
| Agfa-Gevaert | AGFB | 1/06/1999 | 2167 |
| Bekaert | BEKB | 26/04/1996 | 2925 |
| Belgacom | BELG | 30/03/2004 | 947 |
| Cofinimme-Sicafi | COFB | 4/01/1999 | 2254 |
| Colruyt | COLR | 26/04/1996 | 2924 |
| D’Ieteren | DIE | 2/03/2006 | 452 |
| Delhaize Group | DELB | 2/01/1997 | 2761 |
| Dexia | DEXC | 20/11/1996 | 2787 |
| Fortis | FORB | 26/04/1996 | 2925 |
| GBL | GBLB | 26/04/1996 | 2923 |
| Inbev | INB | 21/06/2004 | 828 |
| KBC | KBC | 11/06/1996 | 2854 |
| Mobistar | MOBB | 4/01/1999 | 2263 |
| Nat. Portefeuille | NAT | 2/03/2006 | 452 |
| Omega Pharma | OME | 4/01/1999 | 2251 |
| Solvay | SOLB | 26/04/1996 | 2925 |
| Suez | SZEB | 15/11/2005 | 528 |
| UCB | UCB | 26/04/1996 | 2925 |
| Umicore | UMI | 2/01/1997 | 2763 |
| Total : | 41018 |
– Pour le CAC40 :
| Nom | Symbole | à partir du | nb de cotations |
| Accor | AC | 2/01/1987 | 5254 |
| Air France KLM | AF | 5/01/1999 | 2252 |
| Air Liquide | AI | 2/01/1987 | 5249 |
| Alcaltel-Lucent | ALU | 1/12/2006 | 259 |
| Alstom | ALO | 3/08/2005 | 602 |
| ArcelorMittel | MTP | 20/09/2006 | 311 |
| Axa | CS | 2/01/1987 | 5248 |
| BNP Paribas | BNP | 18/10893 | 3568 |
| Bouygues | EN | 2/01/1987 | 5259 |
| Cap Gemini | CAP | 2/01/1987 | 5254 |
| Carrefour | CA | 2/01/1987 | 5257 |
| Casino Guichard | CO | 2/01/1987 | 5241 |
| Crédit Agricole | ACA | 14/12/2001 | 1527 |
| Danone | BN | 2/01/1987 | 5258 |
| Dexia | DX | 30/11/1999 | 2043 |
| EADS | EAD | 10/07/2000 | 1892 |
| EDF | EDF | 21/11/2005 | 524 |
| Essilor | EF | 2/01/1987 | 5258 |
| France Telecom | FTE | 20/10/1997 | 2569 |
| Gaz de France | GAZ | 8/07/2005 | 620 |
| L’Oréal | OR | 2/01/1987 | 5258 |
| Lafarge | LG | 2/01/1987 | 5256 |
| Lagardère | MMB | 2/01/1987 | 5219 |
| LVMH | MC | 2/01/1987 | 5257 |
| Michelin | ML | 2/01/1987 | 5249 |
| Pernod Ricard | RI | 2/01/1987 | 5253 |
| Peugeot | UG | 2/01/1987 | 5253 |
| PPR | PP | 2/01/1987 | 5227 |
| Publicis Groupe | PUB | 2/01/1987 | 5184 |
| Renault | RNO | 17/11/1994 | 3299 |
| Saint Gobain | SGO | 2/01/1987 | 5251 |
| Sanofi-Aventis | SAN | 2/01/1987 | 5252 |
| Schneider Electric | SU | 2/01/1987 | 5128 |
| Société Générale | GLE | 9/07/1987 | 5121 |
| STMicroelectronics | STM | 24/06/1998 | 2397 |
| Suez | SZE | 2/01/1987 | 5256 |
| Thalès | HO | 2/01/1987 | 5250 |
| Thomson | TMS | 3/11/1999 | 2062 |
| Total | FP | 2/01/1987 | 5260 |
| Unibail-Rodamco | UL | 2/01/1987 | 5256 |
| Vallourec | VK | 2/01/1987 | 5235 |
| Veolia Environ. | VIE | 20/07/2000 | 1885 |
| Vinci | DG | 2/01/1987 | 5255 |
| Vivendi | VIV | 24/04/2006 | 417 |
| Total : | 172925 |
Pour pouvoir comparer tous ces cours de bourse, nous allons les exprimer sous forme de variation journalière, c’est-à-dire la variation par rapport au cours de la veille exprimée en pourcentage. Une fois ces pourcentages obtenus, nous pourrons les répartir selon des intervalles pour chaque instrument et compiler ensuite les résultats obtenus pour le CAC40, le BEL20 et pour l’ensemble des valeurs de notre échantillon.
Nous exprimons cette variation en pourcentage selon la formule suivante :
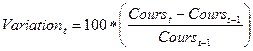 où t est le jour considéré
où t est le jour considéré
Etant donné que nous travaillons sur des données discrètes, nous allons calculer le nombre d’intervalles minimum nécessaire pour être certain de pouvoir exploiter correctement nos données. Pour ce faire, nous allons utiliser la règle de Sturge qui nous donne le nombre de classes minimal k :
![]() où n est le nombre d’observations.
où n est le nombre d’observations.
Dans notre cas, n = 213 940 observations. Nous obtenons donc k = 18,749. Il nous faut donc un minimum de 19 intervalles. Pour plus de précision, nous avons choisi d’utiliser 34 intervalles
Nous avons d’abord découpé les intervalles de -8% à +8% avec un intervalle de 0,5% borné comme suit : Borne inférieure ![]() pourcentage < Borne supérieure.
pourcentage < Borne supérieure.
Nous avons obtenu le résultat suivant pour le CAC40:
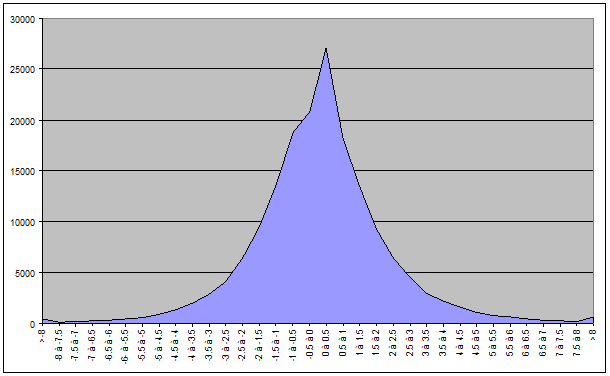
Et le résultat suivant pour le BEL20 :
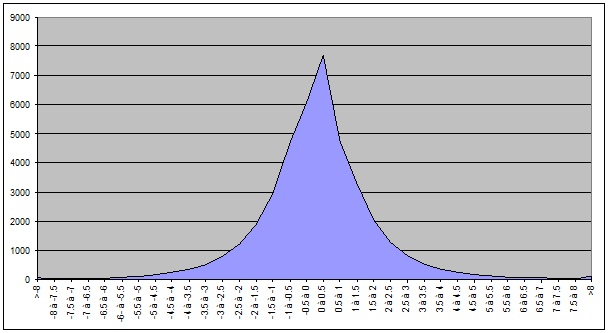
Le résultat consolidé pour les valeurs des deux indices :
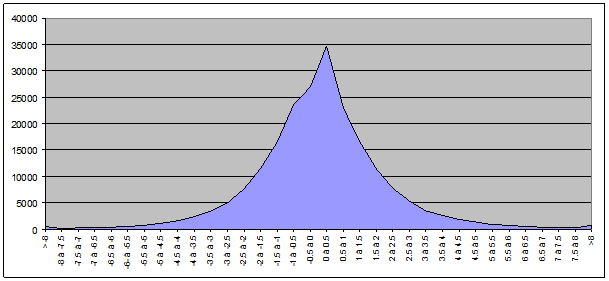
On remarque un comportement étrange de la courbe sur l’intervalle [0 ; 0,5[. On a pic de 5000 cotations en plus que sur l’intervalle précédent [-0,5 ; 0[.
En fait, cela est dû aux cours restés identiques d’un jour à l’autre. Le pic provient du cumul des variations de 0%. Dans notre découpage, pour chaque segment, nous avons inclus la borne inférieure et exclu la borne supérieure, le 0% est donc inclus dans le segment [0 ; 0,5[. Il ne faut pas oublier que nous travaillons sur des valeurs discrètes à deux décimales et non sur des nombres réels. En comparant deux cours de bourse consécutifs à deux décimales, il est fort peu fréquent que le rapport de ces deux chiffres donne un résultat qui correspond très exactement à une des bornes d’un intervalle. Ce qui donc ne devrait pas générer trop d’erreurs sauf dans le cas beaucoup plus fréquent où le cours du jour est égal au cours de la veille. Dans ce cas précis, on tombe très exactement sur la borne 0, ce qui entraîne le pic que nous avons constaté.
Pour vérifier notre théorie, nous avons changé le découpage en le décalant de 0,25 points mais en gardant l’intervalle de 0,5 afin d’inclure le point 0 à l’intérieur d’un intervalle.
Nous obtenons la répartition suivante pour la CAC40 :
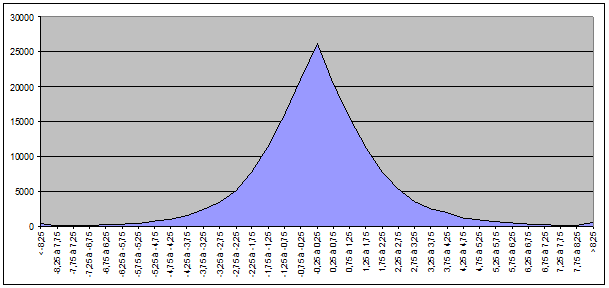
Pour le BEL20 :
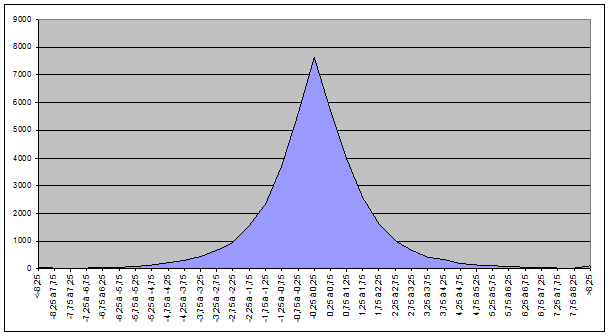
Le résultat consolidé pour les valeurs des deux indices :
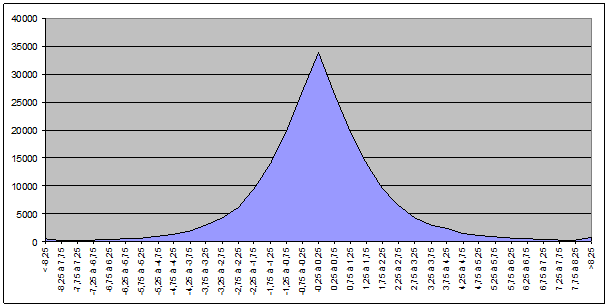
On constate donc que la courbe est plus lissée ce qui tend à confirmer que la variation 0% pose problème.
Malheureusement, avoir un intervalle qui comprend des valeurs positives et négatives n’est pas intéressant au niveau économique puisqu’on mélange des gains et des pertes. Afin de faire disparaître le pic, nous nous proposons de répartir les variations à 0% proportionnellement aux nombres de points présents dans les intervalles [-0,5 ; 0[ et ]0 ; -0,5[. En posant cette condition, nous supposons que la variation de 0% ne tombe pas tout à fait pile sur la borne mais serait par exemple de -0,0000001% ou de +0,0000001%, ce qui inclurait la valeur dans l’un ou l’autre intervalle. Nous avons choisi de la faire proportionnellement au nombre de points dans chaque intervalle par facilité de calcul mais nous aurions pu choisir une toute autre règle de répartition comme par exemple l’intégrer à l’un ou l’autre segment en fonction du signe de cours précédent.
Avec une répartition proportionnelle des variations 0%, nous avons le résultat suivant :
– Pour le CAC40 :
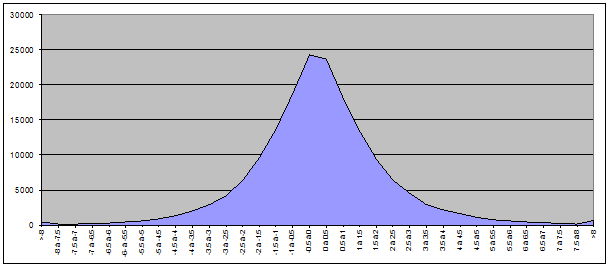
Pour le BEL20 :

Pour le total des valeurs des deux indices :
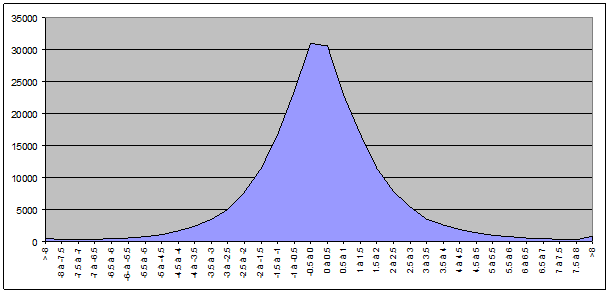
Nous constatons assez aisément que l’allure de cette courbe ressemble assez fort à l’allure d’une distribution de probabilité. Il faut maintenant prouver que cette courbe est bien une distribution de probabilité et identifier quelle distribution.
4.3.3.2. Définition de la distribution de probabilité pour les données utilisées.
On a vu que les courbes obtenues ressemblaient à une distribution de probabilité. On va tenter de définir quelle distribution est la plus proche de nos résultats.
Avant de nous lancer dans nos calculs, observons quelques points particuliers de cette courbe. Tout d’abord, remarquons que les extrémités de la courbe sont relevées.

On pourrait être tenté d’y voir une erreur due à l’usage de valeurs discrètes en nombre fini (donc non infini) et on pourrait augmenter le nombre d’intervalles afin d’aplanir les branches de notre courbe. En pratique, ça ne sert à rien car plus le nombre d’intervalles aux extrémités va augmenter et plus on va avoir des intervalles vides et d’autres avec plusieurs mesures. Donc au lieu de lisser la courbe, cela va plutôt la rendre oscillante aux extrémités.
De plus, il y a lieu de tenir compte de ces valeurs car, économiquement, elles représentent des fortes hausses ou des fortes baisses de valeur. On va voir ci-dessous l’importance de ces grandes variations au niveau de la variation des cours à long terme, celles-ci ont des explications réelles comme des OPA, des hausses ou des baisses de résultats attendues ou non, des splits d’actions, des augmentations de capital, etc. Ces valeurs extrêmes sont donc représentatives de moments importants dans la vie de l’entreprise et on ne peut pas les négliger.
Ceci nous conduit à penser que la distribution de probabilité serait plutôt une distribution leptokurtique qu’une distribution normale. En effet, une distribution leptokurtique est plus pointue que la distribution normale et a des queues plus épaisses :
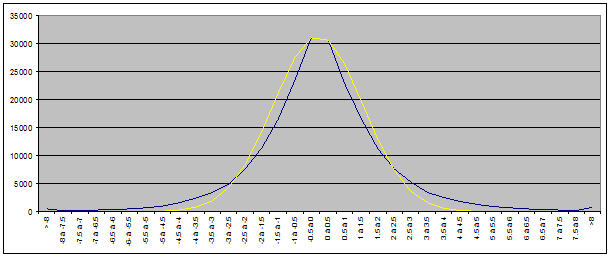
En bleu, la distribution obtenue par mesurage et en jaune une distribution normale.
En fait, la plupart des modèles basés sur le mouvement brownien, par soucis de simplification utilisent une distribution normale. La distribution normale est plus simple à utiliser et mieux connue que d’autres distributions plus complexes à mettre en œuvre des distributions non gaussiennes ![]() -stables, découvertes par Paul Lévy, qui correspondent plus à la réalité. C’est Mandelbrot qui le premier proposa l’utilisation de ces distributions pour rendre compte de ce hasard «sauvage». Mais celles-ci ont un inconvénient majeur, elles décroissent tellement lentement que l’écart-type de ces distributions peut être infini, c’est à dire que la volatilité des cours modélisés par cette distribution est infinie.
-stables, découvertes par Paul Lévy, qui correspondent plus à la réalité. C’est Mandelbrot qui le premier proposa l’utilisation de ces distributions pour rendre compte de ce hasard «sauvage». Mais celles-ci ont un inconvénient majeur, elles décroissent tellement lentement que l’écart-type de ces distributions peut être infini, c’est à dire que la volatilité des cours modélisés par cette distribution est infinie.
Les distributions de lois stables reflètent aussi le fait qu’un petit nombre des meilleures journées contribue à une grande partie de l’augmentation générale sur une longue période. Par exemple, l’indice S&P500 a augmenté de 16,2% entre 1983 et 1992, soit 2526 jours ouvrables. Les 40 meilleurs jours, soit 1,58% de la durée, contribuent à eux seuls à expliquer une hausse de 12,6%, soit 77% de la hausse globale.
Remarquons aussi que la distribution réelle ne peut descendre à gauche que jusqu’à -100% (cas de faillite) tandis qu’elle peut être théoriquement infinie à droite.
Nous allons cependant poser une hypothèse simplificatrice forte et supposer la distribution normale pour le reste de notre exposé. Ceci pour les deux raisons suivantes :
– Nous aurons besoin de cette hypothèse plus loin dans notre développement car la distribution normale est compatible avec le théorème central limite alors qu’une distribution stable non gaussienne ne l’est pas.
– Les méthodologies préconisées par les accords de Bâle II sont aussi basées sur des distributions normales. On peut néanmoins lire ceci : «Les variations des différents facteurs de risque sont toutes distribuées selon une loi normale. Il a été démontré que les principaux facteurs de risque (cours de change, taux d’intérêt, prix des actions) ne suivent pas exactement ce type de distribution. A titre d’exemple, les rendements des actions suivent en réalité une distribution leptokurtique (…). Cette distribution implique que les fluctuations extrêmes (…) surviennent plus fréquemment que ne l’autorise une distribution normale possédant la même volatilité. Il en découle une erreur de modélisation menant à une sous-estimation de la variabilité». La distribution normale est donc utilisée pour les modélisations de solvabilité bancaire préconisées par Bâle II, tout en étant conscient que cela ne correspond pas à la réalité.
4.3.3.3. Réduction des données
Nous allons travailler sur les données obtenues en consolidant la distribution de la variation des cours de nos actions et en répartissant le nombre de variations de 0% entre les variations de l’intervalle avant et après 0.
Ce qui nous donne le tableau de données suivant :
| Intervalle | X | Effectif n | Intervalle | X | Effectif n |
| >-8 | -8 | 517 | 0 à 0.5 | 0,25 | 30603 |
| -8 à -7.5 | -7,75 | 152 | 0.5 à 1 | 0,75 | 22913 |
| -7.5 à -7 | -7,25 | 200 | 1 à 1.5 | 1,25 | 16673 |
| -7 à -6.5 | -6,75 | 278 | 1.5 à 2 | 1,75 | 11343 |
| -6.5 à -6 | -6,25 | 381 | 2 à 2.5 | 2,25 | 7719 |
| -6- à -5.5 | -5,75 | 506 | 2.5 à 3 | 2,75 | 5346 |
| -5.5 à -5 | -5,25 | 712 | 3 à 3.5 | 3,25 | 3482 |
| -5 à -4.5 | -4,75 | 1048 | 3.5 à 4 | 3,75 | 2563 |
| -4.5 à -4 | -4,25 | 1589 | 4 à 4.5 | 4,25 | 1852 |
| -4 à -3.5 | -3,75 | 2374 | 4.5 à 5 | 4,75 | 1295 |
| -3.5 à -3 | -3,25 | 3450 | 5 à 5.5 | 5,25 | 908 |
| -3 à -2.5 | -2,75 | 4953 | 5.5 à 6 | 5,75 | 704 |
| -2.5 à -2 | -2,25 | 7677 | 6 à 6.5 | 6,25 | 526 |
| -2 à -1.5 | -1,75 | 11446 | 6.5 à 7 | 6,75 | 398 |
| -1.5 à -1 | -1,25 | 16532 | 7 à 7.5 | 7,25 | 271 |
| -1 à -0.5 | -0,75 | 23472 | 7.5 à 8 | 7,75 | 194 |
| -0.5 à 0 | -0,25 | 31068 | >8 | 8 | 795 |
Vous trouverez le détail des calculs suivants dans le fichier «Consolidation globale.xls» se trouvant dans les annexes.
– Le mode :
Comme nous le voyons sur la courbe, il n’y a qu’un seul pic, nous sommes donc en présence d’une distribution unimodale.
– La moyenne arithmétique :
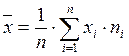 Avec les valeurs
Avec les valeurs ![]() correspondant à la moitié de l’intervalle (sauf pour les extrêmes où nous prendrons -8 et +8), les
correspondant à la moitié de l’intervalle (sauf pour les extrêmes où nous prendrons -8 et +8), les ![]() étant les effectifs des intervalles et n correspondant au total des mesures soit 213 943.
étant les effectifs des intervalles et n correspondant au total des mesures soit 213 943.
Nous obtenons ![]() = 0,05014, soit un nombre positif très proche de zéro puisqu’il s’agit d’une variation de 0,05%. Il est intéressant de remarquer que nous avons une moyenne positive. Cela signifie que nous ne sommes pas centré en zéro mais légèrement décalé vers la gauche. Nous avons donc une tendance croissante moyenne de 0,05014%.
= 0,05014, soit un nombre positif très proche de zéro puisqu’il s’agit d’une variation de 0,05%. Il est intéressant de remarquer que nous avons une moyenne positive. Cela signifie que nous ne sommes pas centré en zéro mais légèrement décalé vers la gauche. Nous avons donc une tendance croissante moyenne de 0,05014%.
– Variance :
![]() avec k=le nombre d’intervalles, soit 34.
avec k=le nombre d’intervalles, soit 34.
Ce qui nous donne une variance de 3,95
– Ecart type :
![]() =
= ![]()
Ce qui nous donne un écart type de 1,98
– Espérance estimée de l’échantillon :
 où
où ![]() est la probabilité de
est la probabilité de ![]()
Ce qui nous donne une espérance de 0,05014. A première vue, cette espérance est égale à la moyenne. On peut expliquer cela du fait que si le nombre de mesures d’un échantillon tend vers l’infini, la moyenne arithmétique tendra vers l’espérance. Or ici nous bénéficions d’une assez grande quantité de mesures, ce qui nous permet d’avoir une très bonne précision sur la moyenne arithmétique.
– Vérification de la règle des 95% :
En principe, +/- 95% des mesures doivent être inclues dans l’intervalle suivant :
![]()
On a : [-3,92 ; 4,02], On va prendre les intervalles [-4 ; +4]. Ce qui représente 201 612 mesures sur un total de 213 943, soit 94,24%. Ce qui est satisfaisant compte tenu du léger décalage entre l’intervalle défini et l’intervalle choisi [-4 ; +4].
4.3.3.4. Vérification de l’indépendance des variations de cours.
Nous allons maintenant vérifier que, tout comme dans un mouvement brownien, nos variations de cours sont indépendantes les uns des autres. Nous allons voir que ce n’est malheureusement pas le cas, ce qui va nous amener à nouveau à poser une forte simplification.
Pour vérifier l’indépendance des cours, il nous a semblé significatif de vérifier comment est distribué le cours de nos actions après une chute ou une hausse de plus de 8%. Nous allons prendre un échantillon dans l’ensemble de nos mesures. Selon le théorème central limite dont nous avons discuté plus haut, si notre ensemble présente une distribution de probabilité, alors notre échantillon devrait aussi vérifier la distribution de probabilité. Et donc, cela signifierait que les cours sont bien indépendants les uns des autres. Si nous n’avons pas une distribution de probabilité sur notre échantillon, cela signifiera que les cours ont bien une mémoire, c’est à dire qu’ils sont influencés par les cours précédents.
Pour ce faire, nous avons pris comme échantillons les cours des jours suivant une baisse de plus de 8% et les cours des jours suivant une hausse de plus de 8%. Nous avons répertorié 504 baisses de plus de 8% et 775 hausses de plus de 8% sur notre échantillon.
Voici les résultats obtenus :
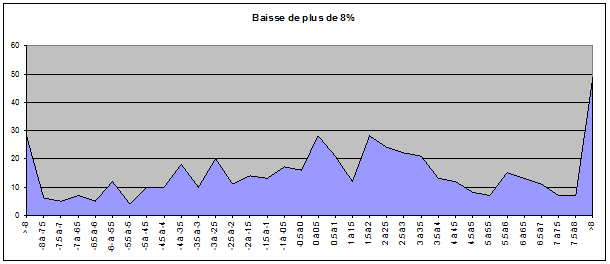
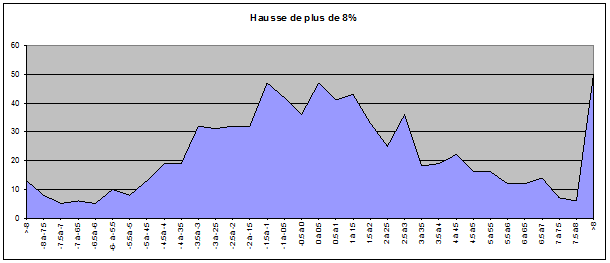
On remarque assez rapidement le fait que les extrémités sont très élevées. On a par exemple répertorié 9.72% de hausses de plus de 8% suite à une chute de plus de 8% et 6.45% de hausses de plus de 8% suite à une hausse de plus de 8%.
Il faudrait probablement affiner les données avec un échantillon plus vaste de façon à avoir une courbe plus lissée. On peut deviner plus ou moins une courbe de Gauss qui se dessine sur le graphe des hausses mais pas grand chose sur le graphe des baisses. Par contre, le fait que nous ayons des queues très anormalement élevées nous montre que nous n’avons pas une distribution de probabilité, ce qui confirmerait que le marché a bien une mémoire et que les cours ne sont pas indépendants les uns des autres.
Ceci reste une démonstration par l’absurde un peu simpliste dans la mesure où on ne s’est basé que sur le cours de la veille et uniquement sur des grandes baisses et des grandes hausses mais cela nous semblait suffisant pour démontrer la non-indépendance des cours les uns par rapport aux autres. On a juste démontré qu’il existait une «mémoire» des cours précédents mais pas de quelle nature était cette mémoire. Il serait intéressant d’étudier ces distributions en fonction de plusieurs cours précédents, de moyennes de cours précédents, etc. afin d’essayer de comprendre comment fonctionne cette mémoire.
Cela étant, pour la suite de notre exposé, nous allons poser une autre hypothèse forte qui est l’indépendance des cours. Ceci est nécessaire pour pouvoir utiliser une distribution de probabilité dans la suite de notre raisonnement. Cependant, gardons à l’esprit que nous avons dû poser cette hypothèse.
4.3.4. Modélisation d’un cours de bourse grâce au mouvement brownien.
Nous avons posé comme hypothèse que les données récoltées pouvaient être traitées comme une distribution de probabilité normale. On a aussi vu que cette distribution de probabilité n’était pas centrée et avait une espérance légèrement positive. On va donc, modéliser le cours aléatoire d’une action selon un mouvement brownien à 1 degré de liberté couplé à une fonction de tendance qui illustre l’espérance non nulle constatée.
4.3.4.1. Générer des nombres aléatoires répartis selon une distribution donnée.
Pour pouvoir faire des tests de modélisation, nous allons devoir générer des nombres aléatoires qui se répartissent selon une loi normale. Or les nombre aléatoires générés par un ordinateur ne sont pas répartis selon une loi normale mais sont générés sur un intervalle ]0;1[ de façon équiprobable, c’est à dire que chaque nombre ou chaque mini-intervalle discret (puisque nous traitons des nombres avec un nombre limité de décimales) a la même probabilité de sortir. Nous voulons donc pouvoir passer ces nombres aléatoires dans une fonction qui nous donnera des nombres aléatoires répartis selon une loi normale.
Nous allons utiliser la formule LOI.NORMALE.INVERSE d’Excell pour faire ces simulations. Vous en trouverez un exemple dans le fichier _Simulation Normale.xls en annexe.
4.3.4.2. Description du modèle
Processus de Wiener ou mouvement brownien classique
Le modèle que nous allons construire, consiste, à chaque itération, à ajouter à la valeur précédente un nombre aléatoire afin de construire une courbe simulant un ensemble de cours de clôture d’un instrument financier.
Prenons un cours qui évolue de façon discrète dans le temps où chaque incrémentation correspond à un jour. Prenons dx la variation de cours de notre action sur une période dt. Les variations sont basées sur une distribution normale.
Un processus de Wiener est caractérisé par :
![]()
– Chaque mouvement aléatoire est indépendant des autres.
– Les mouvements aléatoires sont distribués normalement.
– Une trajectoire continue.
– Le fait qu’il n’est dérivable en quasiment aucun point. (Les seuls points où une dérivée pourrait exister seraient les points intermédiaires entre deux mouvements rigoureusement identiques.)
Un processus de Wiener se défini par l’équation suivante :
![]()
où ![]() est une variable aléatoire distribuée normalement selon N(0,1)
est une variable aléatoire distribuée normalement selon N(0,1)
On peut alors définir l’espérance et la variance de dx :
– L’espérance ![]()
Car ![]() puisque nous avons affaire à une distribution normale centrée réduite.
puisque nous avons affaire à une distribution normale centrée réduite.
– La variance ![]()
– L’écart type est donc ![]()
Selon l’écart type défini, nous pouvons affirmer que l’incertitude augmente avec la racine carrée du temps. Ceci entraîne que l’incertitude sur une action s’atténue avec le temps.
Nous avons réalisé une simulation de variation en pourcentage de cours de bourses sur 500 jours ouvrables à partir d’un cours à 100. Nous obtenons des résultats qui ressemblent à ceci :
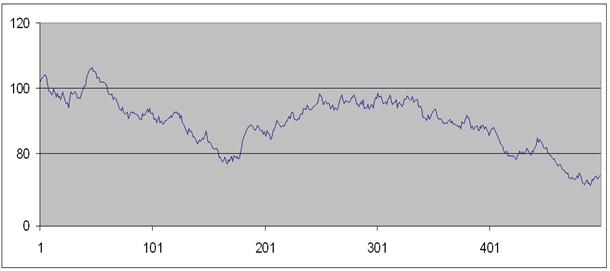
Critique du modèle :
– Dans le modèle que nous venons de décrire, il n’y a pas de trend (= tendance) ou plutôt son trend est nul. C’est à dire que nous ne pouvons pas définir une tendance à long terme ou mieux une espérance à long terme. Nous avons vu dans les cours que nous avons analysés plus haut que l’espérance était légèrement positive de 0,05015. Pour être au plus proche avec la réalité, nous pourrions introduire une tendance dans le modèle.
– La variance est aussi égale à dt, c’est à dire au pas. En effet, nous sommes en présence d’une distribution normale centrée réduite.
Mouvement brownien arithmétique
Pour palier aux lacunes du processus de Wiener, nous allons utiliser une distribution normale classique avec une variance différente de 1 et une espérance non nulle de façon à être plus conforme aux observations.
Nous avons donc le mouvement brownien arithmétique suivant : dx= µ dt + dz
où µ est la tendance, l’écart type et .
On a donc une dominance stochastique à court terme et une dominance du trend à long terme.
On calcule l’espérance et la variance de dx :
– L’espérance :
E(dx)=E(µ dt + dz)= µ dt + E(dz)
E(dx)= µ dt + E(dz) car seul dz est une variable aléatoire
E(dx)= µ dt +
E(dx) = µ dt
– La variance :
V(dx) = V(µ dt + dz)
V(dx) = 0 + ² V(dz)
V(dx) = ² V()
V(dx) = ² dt V()
V(dx) = ² dt
Critique du modèle :
Selon ce modèle, l’écart type reste constant malgré le trend. Dès lors, le rendement total d’une action (x/x) diminuerait avec le temps puisque x resterait constant alors que le prix x augmenterait.
Mouvement brownien géométrique
Le mouvement brownien géométrique permet de rendre compte de l’évolution des rendements des actions.
Si nous définissons le mouvement brownien géométrique par : dx= µ x dt + x dz
Où on multiplie le trend et l’écart-type par x qui est le niveau de prix de l’action.
Si on divise les deux membres par x, on a l’équation suivante :
![]()
Le rendement de notre action est donc décrit par un mouvement brownien géométrique. Ceci implique aussi que le rendement de notre action est indépendant du prix.
Etant donné que le trend est récursif, si =0, on peut définir x au temps t comme ayant la valeur suivante :
![]()
On voit donc que le trend est exponentiel.
Critique du modèle :
On a ici un modèle qui rend assez bien compte de ce que peut donner le cours d’une action. Cependant, les variables µ et sont des constantes, pour améliorer notre modèle, il faudrait pouvoir utiliser des fonctions pour définir ces paramètres.
Processus d’Îto ou mouvement brownien généralisé
Le processus d’Îto est une généralisation du mouvement brownien et intègre des fonctions de tendance et de volatilité. Il se défini par l’équation suivante :
dx = a(x,t) dt + b(x,t) dz
où a(x,t) et b(x,t) sont des fonctions de x et de t qui correspondent respectivement au trend instantané et à la variance instantanée.
On peut calculer l’espérance et la variance de dx :
– L’espérance :
E(dx) = E(a(x,t) dt + b(x,t) dz)
E(dx) = a(x,t) dt + b(x,t) E(dz) or nous avons vu plus haut que E(dz)=0, donc
E(dx) = a(x,t) dt
– La variance :
V(dx) = b² (x,t) dt V()
V(dx) = b²(x,t) dt
Critique du modèle :
Nous avons maintenant un modèle qui représente assez bien la réalité. Il a néanmoins ses limites. En effet, l’ensemble du développement que nous avons réalisé se base sur une distribution normale. Or nous avons vu plus haut que les cours n’ont pas une distribution normale, ceci modifie assez fort les valeurs obtenues dans la mesure où le terme dz n’est plus égal à ![]() dans une distribution normale.
dans une distribution normale.
Une autre limite est la difficulté à définir les fonctions a et b.
4.3.4.3. Utilisation du modèle
Nous avons donc construit un modèle qui nous permet de faire des simulations de cours mais ceux-ci sont tellement aléatoires qu’on peut difficilement évaluer ce que donnera un cours d’ici quelques années.
Nous allons lancer plusieurs fois des simulations de cours avec le même scénario, c’est à dire les mêmes fonctions de tendance a(x,t) et de variance b(x,t). Nous aurons un résultat graphique qui ressemblera à ceci :
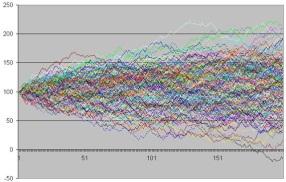
Chaque ligne représente une simulation de cours. On voit que la densité des courbes est plus élevée au milieu et on assiste à une dilution et un éparpillement des probabilités. Il se forme une sorte de cône de probabilité à l’intérieur duquel il est possible que chaque point soit rejoint par le cours de notre action, à des probabilités différentes. Il suffira alors de voir comment se distribuent ces probabilités à un temps t en fonction de la valeur que pourrait prendre notre action.
4.3.4.4. Efficience des marchés
On dit qu’un marché est efficient si le prix des actifs cotés est une évaluation correcte de la valeur de ces actifs, c’est à dire si le prix fixé par le marché «mesure correctement la capacité économique réelle de l’entreprise à faire des profits.» Ce prix serait une estimation qui tienne compte de données comme ses comptes financiers, ses perspectives futures, sa compétitivité, etc. On appellera cette valeur, la valeur fondamentale de l’entreprise. Si les marchés étaient efficients, les prix proposés seraient donc constant et il n’y aurait de variations de prix que lorsque de nouvelles informations seraient disponibles aux acteurs du marché. Les cours évolueraient donc en fonction des informations reçues.
Or, l’existence de bulles spéculatives ou de krachs nous enseigne que les marchés ne sont pas toujours efficients. En fait, outre les données purement économiques disponibles dans la valeur fondamentale, il faut tenir compte d’un facteur psychologique qui impacte les réactions des acteurs du marché. Les décisions des uns influencent les décisions des autres. Ce faisant, si il y a un consensus à la hausse ou à la baisse, même si il n’y a pas de raison logique à ce consensus, les acteurs suivront la tendance et il y aura formation d’une bulle.
Le processus s’explique comme suit : Les différents acteurs n’ont une confiance que relative dans les informations qui sont à leur disposition. Quand ce niveau de confiance est plus ou moins bas, ils ont tendance à s’inspirer des décisions des autres acteurs, pensant que ceux-ci ont de meilleures informations. Ce qui n’est pas toujours le cas, car les autres acteurs sont peut-être aussi dans le même état d’incertitude. Dès lors, si par exemple une tendance haussière se dégage, une majorité des acteurs suivra la tendance en s’inspirant de celle-ci. Ce faisant, ils renforcent eux-mêmes cette tendance à la hausse, confirmant par la même occasion l’idée d’avoir pris la bonne décision et entretenant le phénomène haussier. Même si la hausse est irrationnelle, pourquoi ne pas suivre le mouvement et empocher un bénéfice, plutôt que d’attendre que notre valeur revienne à un niveau normal et perdre une belle occasion. Le phénomène s’auto-entretient par contagion et imitation. La tendance se retournera quand la confiance des acteurs dans les informations haussières données par le marché va se dégrader. Ensuite, suivant le même phénomène, la tendance deviendra baissière et s’auto-entretiendra aussi d’elle-même. En fait, l’information contenue dans les cours n’est pas seulement une information financière sur l’entreprise mais le cours lui-même et sa tendance sont des informations psychologiques utilisées par les humains qui traitent sur le marché. Ce sont ces phénomènes qui sont responsables des fortes hausses ou fortes baisses que nous avons vu dans les queues des distributions étudiées plus haut.
Nous avons vu précédemment que les marchés avaient une mémoire et donc que les cours n’étaient pas indépendants les uns des autres. La non-efficience des marchés pourrait expliquer en partie le fait que les marchés aient une mémoire. Il est aussi heureux que les marchés ne soient pas efficients car c’est ce qui les rend financièrement intéressant et génère des flux de transactions assurant ainsi la liquidité des marchés. Mais cette non-efficience offre aussi la possibilité de «battre le marché». En effet, si les marchés étaient totalement aléatoires, nous serions en face d’un casino et nous ne pourrions espérer faire des gains puisque nous aurions une espérance de gain nulle. On peut donc espérer battre le marché en exploitant ses disfonctionnements comme sa mémoire ou les phénomènes psychologiques d’emballement.
4.3.4.5. Remarques par rapport aux figures de l’analyse technique traditionnelle.
En analyse technique, il existe une série de figures qui aident les analystes à prendre des décisions au moment opportun pour l’achat ou la vente une valeur. En voici une liste non exhaustive basée sur les tracés des cours.
– Les droites de tendance : ce sont des droites imaginaires que les cours ont du mal à franchir. Le cours rebondi plusieurs fois sur ces droites avant de les franchir. Ces droites servent à définir les tendances locales. On les appelle «support» quand le cours est au-dessus de la droite et «résistance» quand le cours est sous la droite. Plus les cours frôlent la droite de tendance, plus celle-ci sera pertinente.
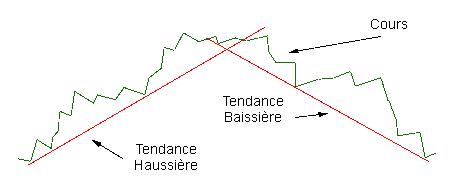
(Source : Edu Bourse, URL : http://www.edubourse.com/guide/guide.php?fiche=tendance-haussiere-baissiere, page consultée le 13/07/08)
– Canaux : un cours peut évoluer entre une droite de support et une droite de résistance.
– Les figures tête-et-épaules : se dit d’une figure représentant trois hausses et baisses successives dont la hausse centrale est la plus importante. Ce qui nous donne une figure comme celle représentée ci-dessous.
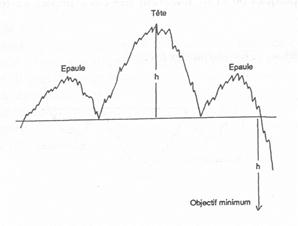
(source : Thierry Béchu, Eric Bertrand et Julien Nebenzahl, L’analyse Technique, Economica, Paris 2008, 558p)
– Les vagues d’Elliott : C’est une théorie qui suppose que le marché évolue de façon cyclique selon une série de huit vagues imbriquées les unes dans les autres à la façon des fractales.
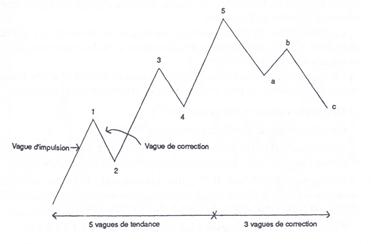
(source : Thierry Béchu, Eric Bertrand et Julien Nebenzahl, L’analyse Technique, Economica, Paris 2008, 558p)
Ayant eu l’occasion de générer pas mal de simulations, j’ai constaté que très souvent sur les graphes issus de ces simulations, nous pouvions appliquer des figures d’analyse technique, comme des tracés de droites de tendance haussière et baissière ou des canaux haussiers et baissiers, en rouge ou même certaines figures en tête-et-épaules en jaune. On y retrouve les vagues d’Elliott, en vert par exemple mais un peu partout sur le tracé.
Par exemple :
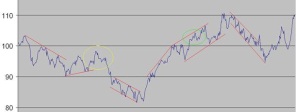
Etant donné que nous pouvons reproduire ce genre d’observations sur des cours totalement fictifs, réalisés sur une base purement statistiques, nous pouvons nous poser des questions sur le bien fondé de certaines figures utilisées par l’analyse technique. Y-a-t-il une explication statistiques à ces figures? Les figures utilisées par les analystes sont-elles vraiment fiables ou est-ce juste le fruit de notre imagination qui nous fait voir ces figures là où il n’y a que du hasard?
Epistémologiquement parlant, il est intéressant que notre modèle reproduise des figures utilisées en analyse technique. En effet, nous arrivons par notre modèle à reproduire des phénomènes observés en analyse technique alors que nous n’avons pas basé l’élaboration de notre modèle sur l’observation de cette discipline. Selon le principe de falsification de Popper expliqué plus haut, ces constatations auraient plutôt tendance à valider la justesse de notre modèle.
4.4. Décodage épistémologique.
L’avènement de la mécanique quantique provoqua un tel chamboulement dans la façon d’envisager le monde, autrement que de façon déterminée, que certains des plus brillants scientifiques comme Einstein eurent beaucoup de mal à se résigner. Ainsi Einstein était persuadé que «Dieu ne joue pas aux dés», ce à quoi Bohr répondait : «Einstein, ne dites pas à Dieu ce qu’il doit faire».
Nous avons vu par des exemples comment fonctionnait la modélisation en mécanique quantique : on réduit les particules élémentaires à des fonctions mathématiques aux propriétés particulières et on travaille ensuite sur les fonctions d’onde et sur des systèmes d’équations pour obtenir des probabilités de trouver une particule à un endroit ou à une vitesse donnée.
Dans notre modélisation de cours d’action, nous avons réduit notre action à une fonction statistique et nous avons ensuite travaillé cette fonction pour obtenir une probabilité de trouver de cours de cette action à un endroit par rapport au temps.
Dans les deux cas, on ne cherche pas à expliquer le pourquoi des phénomènes mais on cherche plutôt à prédire des comportements possibles et probabilistes. Dans le cas de la mécanique quantique, on arrivera à modéliser des comportements de particules mais cette discipline ne permet pas d’expliquer ce qui se passe réellement au niveau atomique. Dans notre modèle, on a supposé que toute l’information disponible était déjà incluse dans le cours de notre action. Une fois le modèle défini, on a la possibilité de prévoir une probabilité de cours après un certain laps de temps mais ce modèle ne donne aucune explication sur la façon dont le prix de cette action pourrait arriver sur un point donné. A vrai dire, on ne s’y intéresse même pas, on cherche juste à décrire un phénomène.
Un autre point commun des deux théories est le fait qu’il est impossible de soumettre ces théories à la reproductibilité expérimentale étant donné que nous travaillons sur des phénomènes probabilistes. On pourra seulement vérifier qu’un phénomène correspond ou non à notre modèle.
Nous avons aussi vu que dans les deux approches, l’observateur n’est pas neutre sur ses observations. Il est observateur et acteur, et dans ce sens, il peut influencer les résultats de ses observations, donc les observations peuvent perdre leur valeur objective et rendre caducs les théories issues de ces observations. Par exemple, dans le cas d’un modèle d’analyse technique, on peut très bien imaginer que quand le modèle nous indique un moment où il faut vendre ou acheter, les analystes suivent les données du modèle et achètent ou vendent, ce qui aura pour effet de renforcer la crédibilité et la fiabilité du modèle, alors que celui-ci pourrait être complètement faux.
Enfin, nous avons encore vu dans le développement de notre modèle à quel point la confrontation de celui-ci avec la réalité était importante. En effet, à chaque étape du processus d’élaboration, nous vérifions la cohérence de notre modèle face à la réalité, nous détectons les imperfections et nous tentons d’y remédier. Il est important de connaître le processus qui a permis d’élaborer notre modèle car cela nous permet d’en connaître les faiblesses et les concessions faites à la réalité pour avoir un modèle utilisable facilement.
4.5. La nécessité de trouver des nouveaux modèles
Les modèles que nous avons développés arrivent à décrire le cours régulier d’une action. Mais nous avons aussi vu qu’ils n’étaient plus pertinents pour expliquer la création de bulles ou de krachs dans la mesure où la modélisation probabiliste ne peut pas tenir compte des phénomènes d’emballement. Nos modèles sont donc efficaces sur le court terme quand le marché n’a pas le temps de s’emballer, ou sur le très long terme quand le marché a le temps de digérer les grandes variations. Il nous faudrait donc pouvoir construire un modèle qui puisse être valable à moyen terme et rendre compte des emballements des cours.
Dans le point suivant, nous allons voir que la théorie du chaos pourrait nous aider à modéliser des hausses ou des baisses prévisibles mais non cycliques. On espère pouvoir utiliser la théorie du chaos pour décrypter les marchés et prévoir à plus ou moins long terme les krachs et les bulles.
Lire le mémoire complet ==> (Comparaison épistémologique entre les modèles issus des sciences de la vie et les modèles de valorisation d’actions)
Mémoire présenté pour l’obtention du grade de Master en sciences commerciales
Enseignement supérieur de type long de niveau universitaire
Groupe ICHEC – ISC St-LOUIS – ISFSC – Haute Ecole


Bonjour. Je souhaites simuler quatre trajectoires discrétisées du mouvement
brownien sur une durée de 2 ans en utilisant un pas de discrétisation d’abord journalier puis 3 fois par jour.
voila ce que je proposes comme code mais je ne vois pas vraiment comment utiliser la notion de temps. merci
t <- seq(0,750,length=750)
for (i in 1:4){
v = matrix(rnorm(log(40)+0.06*t,sd =sqrt((0.20)^(2)*t)))
z = matrix(NA, ncol=750, nrow=5)
Bn <-matrix(log(40)+ 0.12*t +0.20*c(cumsum(v)))
Br <- log(Bn)
plot(t,Br,type="l",xlab="Temps ",col=i,ylim=c(0,4.4))
par(new=T)
print(i)
}