5.2. Bases théoriques de la théorie du chaos
Dans ce paragraphe, nous allons détailler les outils mathématiques dont nous aurons besoin pour élaborer nos modèles.
5.2.1. La dimension fractale ou dimension de Hausdorff.
On peut définir la dimension d’un objet mathématique comme étant le nombre de degré de liberté que possède cet objet, c’est à dire le nombre de références nécessaires pour décrire la position d’un point appartenant à cet objet. Une droite ne possède qu’un seul degré de liberté, un plan en possède deux, etc. Ainsi, un cercle ou un carré a une dimension 1 puisqu’ils ne possèdent qu’un seul degré de liberté.
Lorsqu’on parle de fractale, la notion de dimension change considérablement. Comment situer un point sur une figure qui contient une courbe de longueur infinie dans un espace fini. En fait, la dimension des fractales n’est pas un nombre entier comme 1 ou 2 mais un nombre réel.
L’idée est la suivante : prenons une droite rectiligne. Nous savons que sa dimension est 1. Maintenant, si nous transformons cette droite comme ceci :
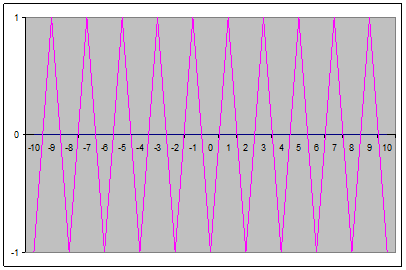
On voit que la distance entre -10 et 10 est beaucoup plus longue sur le ligne brisée rose que sur la ligne bleue, pourtant les deux droites ont une longueur infinie, tout comme les fractales. L’idée de dimension fractale est donc de rendre compte de cette différence de longueur.
Reprenons notre flocon de Koch. A chaque étape de sa construction, on ajoute un triangle. Ce faisant, on rallonge sa longueur de 1 tiers. Donc après n étapes, on aura une longueur de 
. Si n est infini, la longueur sera elle aussi infinie. On voit aussi que la courbe est entièrement incluse dans une surface finie mais étant donné que c’est une ligne, elle devrait être de dimension 1. Le concept de longueur ou de dimension classique n’est donc pas pertinent pour qualifier cette courbe. On utilisera donc le concept de dimension fractale. Ici, la dimension de la courbe n’est pas un entier mais est donnée par la formule développée par Félix Hausdorff :
Où n est le nombre de figures identiques créées par une opération et r est l’échelle de réduction d’une opération.
On peut calculer la dimension du flocon de Koch comme ceci : 
Prenons un autre exemple : le tapis de Sierpinski que nous avons vu ci-dessus. Nous avons un carré divisé en 9 parties dont on retire le milieu. On a donc 8 nouvelles figures identiques. Chaque nouveau carré étant une réduction au tiers du carré central (puisqu’on a 3 carrés par côté). La dimension fractale sera donc :
On sait qu’un plan a une dimension de 2. Le tapis de Sierpinski a une dimension de 1,892 mais s’inscrit dans un plan. On dira qu’il a une dimension topologique de 2. Ceci a amené Mandelbrot à définir les fractales comme des objets dont la dimension était différente de sa dimension topologique.
5.2.2. L’exposant de Lyapunov.
Une des caractéristiques des systèmes chaotiques est la grande sensibilité aux conditions initiales : un petit changement au niveau du point de départ peut entraîner une grande divergence par rapport à un autre point de départ tout proche. L’exposant de Lyapunov va nous permettre de quantifier cette divergence.
Pour illustrer notre raisonnement, nous allons utiliser la fonction logistique développée par un mathématicien belge, Pierre-François Verhulst, en 1830. Cette fonction est destinée à la base à modéliser des évolutions de populations animales. Il s’agit de la fonction :
Où µ est une constante représentative de l’environnement dans lequel évolue notre population.
Pour modéliser l’évolution des populations animales, on avait pour habitude de considérer la population durant une saison comme étant fixe. En effet, les périodes des amours étant très saisonnières, on pouvait considérer qu’après les naissances, la population globale n’évoluait pas beaucoup. Dès lors, on pouvait se permettre de travailler sur des périodes temporelles discrètes.
Les écologistes de l’époque avaient conçu un modèle qui se stabilisait après un certain nombre d’itérations. Pour eux, il était évident qu’une population tend à se stabiliser autour d’un nombre fixé d’animaux, donc le modèle se devait de converger. Et si les observations montraient parfois le contraire, les scientifiques en déduisaient qu’il s’agissait de perturbations extérieures incontrôlables qui modifiaient les conditions de leur modèle, une sorte de bruit blanc parasitaire inévitable.
Cette équation est très stable tant que le cœfficient µ reste entre 0 et 3. Au delà, notre fonction nous donne des résultats tout à fait erratiques. A l’époque, les scientifiques jugeaient donc ce modèle valide tant que µ restait entre 0 et 3.
Ci-dessous, un graphe représentant l’évolution de la fonction selon que le paramètre µ soit entre 0 et 3 et plus grand que 3. On voit bien que la fonction converge tant que µ est inférieur à 3. Après, la fonction commence à diverger et plus µ augmente, plus la divergence est élevée. Nous allons donc étudier le chaos généré avec un paramètre µ=4.
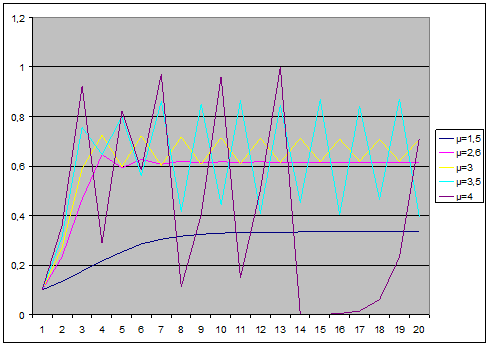
On constate effectivement que pour µ<3, la courbe se stabilise autour d’une seule valeur. A µ=3, la courbe oscille entre deux valeurs différentes (deux attracteurs), à µ=3,5 la courbe oscille aussi entre quatre attracteurs et à µ=4, le comportement est chaotique.
On s’est rendu compte que des modèles chaotiques ainsi créés pouvaient donner des résultats correspondants à la réalité. Ainsi les courbes d’épidémie de certaines maladies peuvent réagir selon un schéma chaotique identifié.
Nous allons regarder comment une petite variation du point de départ va générer une grande divergence. Pour l’équation 
, 0,75 est tout à fait stable. Voici ce que donne la courbe pour 0.749, 0.7499 et 0.751 :
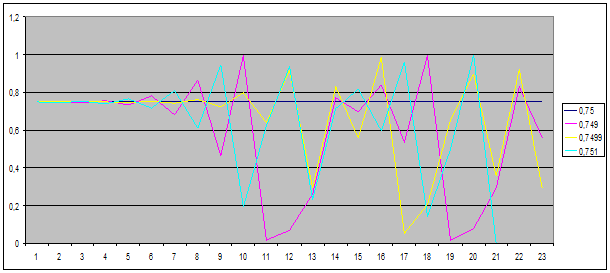
On voit que sur les premières itérations, nous avons un résultat semblable. Ce qui nous aide à déterminer l’exposant de Lyapunov, c’est la durée de «fiabilité de notre fonction par rapport à une variation de conditions initiales donnée.
Prenons : d, la divergence par rapport à un point de référence ; t, le temps ; i, l’erreur initiale et L, l’exposant de Lyapunov.
On a l’équation : 
Si l’exposant L est négatif, alors l’équation ci-dessus est convergente et donc, nous ne sommes pas dans une situation de chaos. Il faut donc que cet exposant soit positif.
Nous n’allons pas rentrer en détail dans les calculs de l’exposant mais relevons sa définition qui est la moyenne de la valeur absolue du log de sa dérivée, soit :
5.2.3. Les bifurcations de Feigenbaum
Reprenons notre équation logistique 
avec µ, une constante. On a vu plus haut que selon la valeur de µ, on pouvait avoir des valeurs de x qui convergent soit vers un point, soit vers plusieurs points, soit qui ne converge pas du tout. Nous allons tracer le diagramme de Feigenbaum qui consiste à chercher les valeurs vers lesquelles x converge en fonction de µ. On a le graphe suivant, avec µ en abscisse et en ordonné les valeurs de convergence :
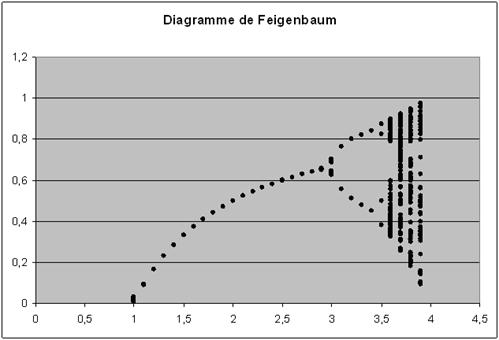
Ci-dessous, un diagramme plus précis. En zoomant sur certaines parties, on se rend compte que le diagramme de Feigenbaum est une fractale.
(Source : Darren Abbey, Feigenbaums Diagrams, URL : www.ganymeta.org/~darren/bifurcation.php, page consultée le 24/07/08)
Lire le mémoire complet ==> (Comparaison épistémologique entre les modèles issus des sciences de la vie et les modèles de valorisation d’actions)
Mémoire présenté pour l’obtention du grade de Master en sciences commerciales
Enseignement supérieur de type long de niveau universitaire
Groupe ICHEC – ISC St-LOUIS – ISFSC – Haute Ecole
