Résultats économétriques, fonction de production agricole
IV- Résultats économétriques
Nous cherchons donc à mettre en lumière l’impact de la composition du collectif de travail sur la productivité moyenne des exploitations ainsi que les efficiences relatives de trois types de main-d’œuvre : familiale, salariée permanente et salariée saisonnière.
Pour ce faire, nous nous fondons sur une fonction de production de type Cobb-Douglas que nous estimons en panel sur des données individuelles d’exploitations de fruits et légumes du RICA de 1995 à 2006.
Nous présentons dans un premier temps les résultats de notre estimation et leurs interprétations. Dans un second temps, nous présentons un certain nombre de tests de robustesse que nous avons mis en œuvre.
IV.1 – Estimation de la fonction de production
Nous estimons la fonction de production avec et sans les variables de composition du collectif de travail afin de savoir si l’introduction de ces variables dans le modèle est pertinente et nécessaire. Les résultats de ces deux estimations sont présentés dans le Tableau 60.
Tableau 60- Résultats de l’estimation en panel avec effets fixes
| Estimation sans prise en compte de la composition du collectif de travail | Estimation avec prise en compte de la composition du collectif de travail | |
| VARIABLES | logVA | logVA |
| logK | 0.077*** (0.020) | 0.077*** (0.020) |
| logSAU | 0.047 (0.039) | 0.053 (0.039) |
| logL | 0.707*** (0.048) | 0.580*** (0.055) |
| Rperm | 0.380*** (0.137) | |
| Rsais | 0.552*** (0.129) | |
| Année 1995 | -0.065 (0.045) | 0.015 (0.049) |
| Année 1996 | -0.138*** (0.043) | -0.065 (0.047) |
| Année 1997 | -0.114*** (0.044) | -0.046 (0.046) |
| Année 1998 | -0.205*** (0.044) | -0.136*** (0.046) |
| Année 1999 | -0.240*** (0.042) | -0.175*** (0.045) |
| Année 2000 | -0.080** (0.040) | -0.017 (0.043) |
| Année 2001 | -0.147*** (0.041) | -0.088** (0.043) |
| Année 2002 | 0.017 (0.040) | 0.019 (0.039) |
| Année 2003 | -0.168*** (0.042) | -0.164*** (0.042) |
| Année 2004 | 0.007 (0.037) | 0.009 (0.037) |
| Année 2005 | 0.001 (0.035) | -0.001 (0.035) |
| Année 2006 | ref | ref |
| Constante | 3.921*** (0.431) | 4.749*** (0.464) |
| Observations | 3916 | 3916 |
| Nb d’individus | 730 | 730 |
| R2 | 0.136 | 0.143 |
Écarts- types robustes entre parenthèses
*** p<0.01, ** p<0.05, * p<0.1
La modélisation en panel à effets fixes est adaptée à nos données : d’une part, nous devons considérer la dimension de panel des données (double dimension temporelle et individuelle) car l’hypothèse d’absence d’effets individuels241 est rejetée au seuil de 1% (test de Fisher).
D’autre part, les effets individuels doivent être modélisés par des effets fixes et non par des effets aléatoires. En effet, la modélisation en effets aléatoires exige qu’il y ait indépendance entre les effets individuels et les variables explicatives.
Or, l’hypothèse d’indépendance est rejetée au seuil de 1% (test d’Hausman). Le modèle à effets fixes est donc préférable au modèle à effets aléatoires.
Nous détectons de l’hétéroscédasticité dans nos données mais pas d’autocorrélation. Nous corrigeons donc pour l’hétéroscédasticité242.
L’introduction des variables de composition du collectif de travail Rperm et Rsais est pertinente puisque, d’après le test du rapport de vraisemblance entre les modèles avec et sans les variables (Likelihood Ratio test), l’hypothèse de nullité des coefficients de ces variables est rejetée au seuil de 1%.
Les coefficients des variables de composition de la force de travail Rperm et Rsais sont tous deux significatifs. La productivité des exploitations est donc corrélée à la composition de leur collectif de travail.
Les résultats des estimations montrent, d’une part, que l’élasticité de la production par rapport au facteur terre n’est pas significative et, d’autre part, que l’élasticité de la production par rapport au travail (0,71 et 0,58) est beaucoup plus forte que l’élasticité de la production par rapport au capital (0,08).
Ce résultat est à mettre en lien avec le fait que le secteur des fruits et légumes est un secteur extrêmement intensif en travail et moins intensif en capital et surtout en terre.
Les coefficients associés aux facteurs de production sont inférieurs à 1, il y a donc bien décroissance des productivités marginales. La somme de ces coefficients est, quant à elle, inférieure à 1, les rendements d’échelle sont donc décroissants.
On peut noter que la prise en compte de la composition du collectif de travail tend à réduire l’élasticité de la production par rapport au travail mais ne modifie pas celle du capital.
Ce résultat montre que la composition du collectif de travail est peu corrélée au niveau de capital et assez fortement corrélée à la quantité globale de travail : plus la quantité globale de travail augmente, plus la part de travail salarié s’accroît. Ce résultat est en lien avec le caractère limité de la quantité de travail familial disponible.
Les coefficients d’efficience relative (ou de productivité marginale) des travailleurs permanents et des travailleurs saisonniers par rapport aux travailleurs familiaux (respectivement 1 et 1) sont des transformations des coefficients estimés des variables Rperm et Rsais, (respectivement et ).
Ils sont calculés, ainsi que leur variance, leur écart-type et leur niveau de significativité par la méthode Delta (voir [Greene, 2000] p. 357-358243).
Le Tableau 61 présente les résultats de ces calculs.
Tableau 61- Coefficients d’efficience relative des permanents 1 et des saisonniers 1
| Coefficients d’efficience relative | Coef. | Std. Err. | t | P>t | [95% Conf. Interval] | ||
| Travailleurs permanents | 1 | 1,655 | 0,274 | 6,050 | 0,000 | 1,119 | 2,19 |
| Travailleurs saisonniers | 1 | 1,951 | 0,277 | 7,040 | 0,000 | 1,407 | 2,49 |
Nous rappelons que le coefficient d’efficience relative des permanents (ou des saisonniers) est le rapport entre la productivité marginale des travailleurs salariés permanents (ou saisonniers) et celle des travailleurs familiaux, elle-même normalisée à 1.
Le coefficient d’efficience relative des travailleurs permanents est significativement supérieur à un 1 1 244. La productivité des travailleurs salariés permanents est donc significativement supérieure à celle des travailleurs familiaux.
De même, la productivité des salariés saisonniers est significativement supérieure à celle des travailleurs familiaux 1 1 245.
Nous avons distingué, dans notre analyse, les travailleurs salariés permanents des travailleurs salariés saisonniers. Les travailleurs permanents ne sont pas employés uniquement à des périodes où la productivité du travail est grande. Ils sont vraisemblablement employés toute l’année comme les travailleurs familiaux.
Dès lors, si les différences saisonnières de productivité du travail peuvent expliquer la différence de productivité entre les travailleurs salariés saisonniers et les travailleurs familiaux, comme le suggéraient A. Deolalikar et W. Vijverberg [1987], elle ne peut expliquer la différence de productivité entre les travailleurs salariés permanents et les travailleurs familiaux que nous mettons en avant.
Cette différence de productivité entre les salariés permanents et la famille est dans la lignée des travaux empiriques précédents dont les résultats suggèrent que les exploitations familiales sont moins efficientes que les exploitations avec salariés du fait d’une plus grande division du travail dans les exploitations à salariés [Latruffe et al., 2004 ; Lambarraa et al., 2007 ; Zhu et al., 2008 ; Lambarraa et al., 2009].
La moindre productivité des travailleurs familiaux par rapport aux salariés permanents que nous mettons en avant pourrait donc s’expliquer par le fait que les travailleurs familiaux sont moins spécialisés.
Les gains de productivité liés à la division du travail et à la spécialisation des tâches sembleraient dépasser les pertes de productivité liées à l’aléa moral des travailleurs salariés dans les exploitations que nous étudions.
La comparaison des coefficients d’efficience relative des travailleurs salariés permanents et des travailleurs salariés saisonniers montre que les saisonniers sont plus productifs que les permanents. Cette différence est significative au seuil de 5% 246.
Nous nous attendions à ce que les travailleurs permanents soient plus productifs que les travailleurs saisonniers du fait de leur capital humain spécifique et de leur coût d’opportunité élevé à être licenciés.
Plusieurs raisons sont susceptibles d’expliquer la plus forte productivité du travail salarié saisonnier par rapport travail salarié permanent.
D’une part, les saisonniers sont, pour la plupart, employés pendant les périodes de fortes activités au cours desquelles la productivité marginale du travail est grande.
Les travailleurs permanents peuvent être sous- employés à certaines périodes de l’année et peuvent dès lors être moins productifs. Cet argument est celui mis en avant par A. Deolalikar et W. Vijverberg [1987].
Cependant, notre résultat est susceptible d’être expliquer d’une autre manière. En effet, comme nous l’avons vu précédemment, le secteur agricole, et plus particulièrement le secteur des fruits et légumes, présente un certain nombre de spécificités concernant le travail saisonnier.
D’une part, malgré le caractère temporaire du contrat, il existe souvent une continuité dans la relation de travail unissant les travailleurs saisonniers à une exploitation [Lamanthe, 2005].
Ils Les travailleurs saisonniers reviennent souvent d’une année sur l’autre chez le même employeur. Ils sont donc susceptibles d’accumuler, au même titre que les travailleurs permanents, des connaissances spécifiques et des savoirs tacites propres à l’exploitation.
De plus, certains contrats temporaires, comme le contrat d’immigration temporaire, ou contrat OMI, sont susceptibles d’être extrêmement incitatifs.
Pour ce type de contrat, le droit de séjour en France est attaché au contrat de travail. En cas de rupture du contrat, le travailleur doit quitter le territoire et peut avoir des difficultés à revenir l’année suivante.
Ainsi, pour ces travailleurs, le coût d’opportunité d’être licenciés est très élevé et le contrat est très incitatif. Dès lors, la plus grande productivité des travailleurs saisonniers peut être en lien avec l’originalité des formes d’emploi temporaire du secteur agricole.
IV.2- Tests de robustesse
Afin de tester la robustesse de nos résultats, nous avons fait plusieurs séries d’estimations supplémentaires. Ces estimations ont pour but de vérifier la robustesse de nos résultats sur plusieurs points : d’une part, par rapport aux biais d’échantillonnage et par rapport à la non prise en compte de la pondération, d’autre part, par rapport à la prise en compte du passage aux 35 heures, et, enfin, par rapport à deux problèmes récurrents de l’estimation des fonctions de production : le problème d’endogénéité des variables explicatrices et celui de la spécification de la forme de la fonctionnelle.
Pour l’ensemble de ces estimations, les coefficients des indicatrices annuelles ne sont pas reportés dans les résultats afin d’en simplifier la lecture. Ces indicatrices sont cependant toujours incluses comme variables explicatives.
Les premières estimations ont pour but de vérifier que nos résultats sont robustes malgré une modification dans l’échantillonnage.
D’une part, nous estimons notre modèle en considérant un panel cylindré, c’est-à-dire en ne conservant que les exploitations qu’il est possible de suivre sur douze ans, soit 52 exploitations.
Le panel cylindré permet de mieux capter la variabilité intra-annuelle de chaque individu mais introduit un biais de cylindrage. Comme le montre le Tableau 62, les résultats de cette estimation sont similaires à ceux présentés précédemment.

D’autre part, nous estimons notre modèle en excluant les exploitations ne répondant pas à un critère strict de définition de l’exploitation familiale.
Nous considérons le critère de Raup [1986] selon lequel une exploitation familiale emploie moins de 1,5 UTA salariées. Là encore, les résultats sont similaires à ceux de notre estimation principale (voir Tableau 62).
Tableau 62- Résultats des estimations en panel (effets fixes) sur des échantillons différents
| Echantillon en panel cylindré | Echantillon avec exploitations familiales au sens strict (Critère de Raup) | |
| VARIABLES | logVA | logVA |
| logK | 0.109*** (0.029) | 0.067** (0.027) |
| logSAU | 0.088 (0.073) | 0.034 (0.068) |
| logL | 0.414*** (0.083) | 0.352*** (0.105) |
| Rperm | 0.521** (0.223) | 0.429* (0.262) |
| Rsais | 0.651*** (0.205) | 0.694*** (0.214) |
| Constante | 5.894*** (0.701) | 6.615*** (0.850) |
| Observations | 624 | 1585 |
| Nb d’individus | 52 | 369 |
| R2 | 0.183 | 0.074 |
Écarts-types robustes entre parenthèses
*** p<0.01, ** p<0.05, * p<0.1
Indicatrices annuelles incluses dans la régression
La deuxième vérification que nous effectuons concerne le biais susceptible d’être introduit par la non prise en compte de la pondération.
L’estimation en effets fixes n’autorise pas la pondération des observations sous STATA 10, le logiciel que nous utilisons.
Pour cerner au mieux l’impact de la pondération sur nos résultats, nous faisons l’estimation en pooled, avec et sans pondération, afin de voir si les résultats sont significativement modifiés par la prise en compte des pondérations.
L’estimation en pooled sur données de panel ne décompose pas le terme d’erreurs en un effet individuel et un effet idiosyncratique comme le fait l’estimation en effets fixes (ou aléatoires). Il tient compte cependant de la corrélation intra-individuelle des erreurs.
L’estimation en pooled est donc moins précise que l’estimation en effets fixes étant donné qu’elle ne permet pas d’isoler l’influence des facteurs inobservables des individus sur leur comportement dès lors que ces facteurs restent stables dans le temps.
Nous introduisons dans la régression pooled certaines variables dont nous disposons afin de contrôler au mieux les caractéristiques stables dans le temps :
- l’OTEX (otes OTEX serre, otef OTEX fruits, otem OTEX maraîchage, otems OTEX serre et maraîchage),
- le régime de travail (s00=1 si l’exploitation est sans main-d’œuvre salariée, 0 sinon),
- la formation agricole de l’exploitant (fa=1 si l’exploitant a une formation agricole supérieure au secondaire, 0 sinon) et sa formation générale (fg=1 si l’exploitant a une formation générale supérieure au secondaire, 0 sinon).
Les résultats sont présentés dans Tableau 63. Ils montrent, d’une part, que l’estimation en pooled donne des résultats similaires à l’estimation en effets fixes et, d’autre part, que la prise en compte ou non de la pondération ne modifie pas significativement les résultats. La surreprésentation des grandes exploitations dans notre échantillon n’affecte donc pas nos résultats.
Tableau 63- Résultats des estimations en pooled avec et sans pondération
| Avec pondération | Sans pondération | |
| VARIABLES | logVA | logVA |
| logK | 0.129*** (0.006) | 0.148*** (0.007) |
| logSAU | -0.020*** (0.007) | -0.003 (0.008) |
| logL | 0.848*** (0.013) | 0.833*** (0.015) |
| Rperm | 0.440*** (0.039) | 0.278*** (0.043) |
| Rsais | 0.537*** (0.037) | 0.360*** (0.042) |
| fa | -0.111*** (0.018) | -0.054*** (0.015) |
| fg | 0.105*** (0.020) | 0.048** (0.019) |
| s00 | 0.038 (0.021) | -0.085*** (0.025) |
| otef | ref | ref |
| otes | 0.274*** (0.018) | 0.290*** (0.020) |
| otems | 0.348*** (0.023) | 0.312*** (0.025) |
| otem | 0.256*** (0.016) | 0.248*** (0.016) |
| Constante | 1.841*** (0.110) | 1.846*** (0.120) |
| Observations | 3916 | 3916 |
| Nb d’individus | 730 | 730 |
| Log-likelihood | -1145 | -1822 |
Écarts-types entre parenthèses
*** p<0.01, ** p<0.05, * p<0.1
Indicatrices annuelles incluses dans la régression
La troisième vérification que nous faisons concerne le passage aux 35h et sa prise en compte dans les données du RICA.
L’introduction, conjointement aux indicatrices annuelles, d’une indicatrice prenant la valeur 1 avant le passage aux 35h et 0 après (ante) ne modifie pas les résultats de l’estimation comme le montre le Tableau 64. Le coefficient de cette indicatrice n’est pas significatif.
Tableau 64- Résultats des estimations panel (effets fixes) avec la variable indicatrice du passage aux 35h
| VARIABLES | logVA |
| logK | 0.077*** (0.020) |
| logSAU | 0.053 (0.036) |
| logL | 0.580*** (0.046) |
| Rperm | 0.380*** (0.119) |
| Rsais | 0.552*** (0.111) |
| Ante | -0.065 (0.045) |
| Constante | 4.749*** (0.405) |
| Observations | 3916 |
| Nb d’individus | 730 |
| R2 | 0.143 |
Écarts-types entre parenthèses
*** p<0.01, ** p<0.05, * p<0.1
Indicatrices annuelles incluses dans la régression
La quatrième vérification que nous menons concerne la possible endogénéité de nos variables explicatives. Le problème d’endogénéité est un problème classique et récurrent dans l’estimation des fonctions de production (voir entre autres [Griliches et Mairesse, 1998]).
Il est lié à la simultanéité des prises de décision des exploitants concernant la variable endogène (le niveau de production) et les variables exogènes (inputs).
Nous cherchons à instrumenter les variables supportant le plus grand risque d’endogénéité, à savoir les variables concernant le facteur travail (quantité de travail Lit et composition de la main-d’œuvre Rpermit et Rsaisit).
Notre base de données comporte un nombre relativement faible de variables. De plus, les caractéristiques du marché du travail local disponibles dans d’autres bases statistiques247 ne sont pas suffisamment corrélées à la composition de la force de travail sur les exploitations.
Nous remplaçons donc nos variables par leurs valeurs retardées de deux ans248 (laglogL, lagRperm et lagRsais) pour tenter de corriger l’endogénéité. Les résultats de cette estimation sont présentés dans le Tableau 65.
Certaines de nos variables retardées perdent leur significativité. Le coefficient de la part du travail saisonnier reste significativement positif. La plus grande efficience des travailleurs saisonniers est donc un résultat robuste.
Tableau 65- Résultats des estimations en panel (effets fixes) avec des variables retardées
| VARIABLES | logVA |
| logK | 0.139*** (0.036) |
| logSAU | 0.152** (0.062) |
| laglogL | 0.064 (0.083) |
| lagRperm | 0.236 (0.183) |
| lagRsais | 0.311* (0.173) |
| Constante | 8.527*** (0.718) |
| Observations | 2456 |
| Nb d’individus | 563 |
| R2 | 0.049 |
Écarts-types robustes entre parenthèses
*** p<0.01, ** p<0.05, * p<0.1
Indicatrices annuelles incluses dans la régression
La moindre significativité de ces résultats est vraisemblablement liée au fait que ces variables retardées sont finalement de mauvais instruments.
En effet, nous avons fait une estimation panel IV (instrumental-variables) avec ces variables comme instruments. Dans la première étape de la régression, c’est-à-dire dans la régression des variables exogènes et de l’instrument sur la variable suspectée d’être endogène, ces instruments ne sont pas significatifs.
La dernière vérification que nous menons concerne la forme de la fonction de production.
En premier lieu, nous regardons si les estimations devaient être faites séparément selon les différentes OTEX, c’est-à-dire si les fonctions de production devaient être considérées comme différentes entre les OTEX étudiées.
Nos résultats montrent que les coefficients ne varient pas significativement entre l’estimation sur l’ensemble des OTEX et l’estimation sur chacune des OTEX séparément (test de Chow). Ce résultat est rassurant quant au biais de notre échantillon en faveur des exploitations légumières que nous avons souligné précédemment.
Dans un deuxième temps, nous considérons la spécification de la fonction de production à proprement parlé. Bien que la fonction de production Cobb-Douglas soit souvent utilisée dans les études empiriques sur la main-d’œuvre en agriculture (voir par exemple A. Deolalikar et W. Vijverberg [1983 ; 1987], G. Frisvold [1994]), elle repose sur des hypothèses restrictives, notamment celle de l’élasticité de substitution unitaire entre les facteurs de production.
Cette hypothèse s’avère relativement forte dans le secteur que nous étudions. En effet, comme nous l’avons vu précédemment, la substitution entre le capital et le travail dans ce secteur semble relativement faible.
Il existe d’autres formes de fonction de production appelées « flexibles » qui n’imposent pas ce type de restriction. La fonction flexible la plus couramment utilisée est la fonction Translog [Christensen et al., 1971] :
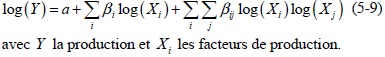
Dans cette fonction de production, l’élasticité des facteurs dépend du niveau des facteurs et l’élasticité de substitution entre facteurs n’est pas fixée à priori.
La mesure que nous avons retenue du facteur travail, le travail efficient ou effectivement productif L* , a l’avantage majeur de permettre une estimation des paramètres qui nous intéressent, à savoir les efficiences relatives des différents types de main-d’œuvre.
Cependant, elle présente l’inconvénient de conduire à des estimations non linéaires. Dans le cas simple d’une fonction de production de type Cobb-Douglas, les estimations peuvent être aisément approximées par des estimations linéaires249. C’est pourquoi cette forme de fonction de production est la plus souvent mise en œuvre.
241 Ou d’une unique intercepte commune.
242 Commande Robust du logiciel STATA.
243 Commande STATA nlcom.
244 est supérieur à zéro au seuil de 1% (Méthode Delta).
245 est supérieur à zéro au seuil de 1% (Méthode Delta).
246 La différence entre les deux coefficients d’efficience relative est aussi recalculée par la méthode Delta.
247 Caractéristiques des Bassins de vie, utilisées dans le chapitre précédent.
248 L’estimation en effet fixe se faisant par différence, le retard considéré doit être de deux années et non d’une seule année.
249 Cette approximation est faite par le biais d’un développement limité entre les équations (5-6) et (5-7) du II de ce chapitre.
Une fonction Translog peut aussi être estimée. Elle est dans ce cas soit non linéaire soit elle se fait au prix de restrictions non linéaires imposées sur les paramètres [Sevestre, 1990 ; Crepon et Mairesse, 1993].
Nous avons fait une estimation en considérant une forme Translog. Les résultats de cette estimation sont présentés dans le Tableau 66.
Dans cette estimation, aucun des trois facteurs de production considérés (capital, travail et terre) n’est plus significatif et le signe du coefficient de la part du travail saisonnier s’inverse. Les termes d’interaction sont parfois significatifs suggérant, par exemple, que l’impact de la part de travail saisonnier croît avec la quantité de travail.
Cette estimation nous semble cependant peu pertinente. En effet, les problèmes de multicolinéarité, courants dans l’estimation des fonctions de production de type Translog, sont susceptibles d’être particulièrement marqués dans notre cas.
La décomposition de la quantité de travail que nous avons faite entraîne des niveaux de corrélations entre les variables supérieurs à 99% (voir Tableau 67).
Pour détecter plus précisément la multicolinéarité, nous avons calculé, en cross-section, la mesure du changement de la variance de chacun des facteurs lorsqu’ils sont introduits dans la régression.
Cette mesure, notée VIF, Variance Inflation Factor, doit être inférieure à 10 pour chaque variable et en moyenne proche de 1 [Cahuzac et Bontemps, 2008] (p.87). Dans le cas de l’estimation de la fonction Translog, la moyenne des VIF est de 348 et les plus grandes VIF sont supérieures à 1000.
Le même test dans le cas d’une fonction de production de type Cobb-Douglas donne une moyenne des VIF de 3.
La mutlicolinéarité entraînant la non-convergence des estimateurs et donc leur faible précision, nous préférons donc la spécification de la fonction de production de type Cobb-Douglas.
Tableau 66- Résultats de l’estimation en panel (effets fixes) d’une fonction de production de type Translog
| VARIABLES | logVA |
| logK | 0.288 (0.287) |
| logSAU | -0.196 (0.334) |
| logL | 0.169 (0.961) |
| Rperm | -2.562 (2.160) |
| Rsais | -3.896** (1.888) |
| logK^2 | 0.027*** (0.006) |
| logL^2 | 0.047 (0.060) |
| logSAU^2 | 0.013 (0.019) |
| Rperm^2 | -0.296 (0.399) |
| Rsais^2 | -0.970** (0.388) |
| logK*logL | -0.077** (0.035) |
| logK*logSAU | -0.024 (0.015) |
| logK*Rperm | -0.040 (0.100) |
| logK*Rsais | -0.065 (0.080) |
| logL*Rperm | 0.438* (0.258) |
| logL*Rsais | 0.677*** (0.234) |
| logL*logSAU | 0.046 (0.040) |
| logSAU*Rperm | 0.108 (0.101) |
| logSAU*Rsais | 0.104 (0.086) |
| Rperm*Rsais | -2.094*** (0.713) |
| Constante | 6.328 (4.451) |
| Observations | 3916 |
| Nb d’individus | 730 |
| R2 | 0.164 |
Écarts-types robustes entre parenthèses
*** p<0.01, ** p<0.05, * p<0.1
Indicatrices annuelles incluses dans la régression
Tableau 67- Tableau des corrélations entre les variables explicatives de la fonction de production de type Translog
| logK | logK^2 | logSAU | logL | logL^2 | logK* logL | logK* Rperm | logK* Rsais | logL* Rperm | logL* Rsais | Rperm* Rsais | Rperm | Rsais | logSAU *logL | logK* logSAU | logSAU *Rperm | logSAU *Rsais | |
| logK | 1.000 | ||||||||||||||||
| logK^2 | 0.994* | 1.000 | |||||||||||||||
| logSAU | 0.378* | 0.378* | 1.000 | ||||||||||||||
| logL | 0.514* | 0.533* | 0.354* | 1.000 | |||||||||||||
| logL^2 | 0.516* | 0.536* | 0.360* | 0.998* | 1.000 | ||||||||||||
| logK*logL | 0.886* | 0.895* | 0.420* | 0.850* | 0.852* | 1.000 | |||||||||||
| logK*Rperm | 0.308* | 0.322* | 0.039* | 0.413* | 0.410* | 0.411* | 1.000 | ||||||||||
| logK*Rsais | 0.360* | 0.363* | 0.342* | 0.542* | 0.540* | 0.509* | -0.3061* | 1.000 | |||||||||
| logL*Rperm | 0.268* | 0.281* | 0.035* | 0.425* | 0.423* | 0.391* | 0.9946* | -0.306* | 1.000 | ||||||||
| logL*Rsais | 0.308* | 0.310* | 0.338* | 0.564* | 0.563* | 0.489* | -0.3030* | 0.993* | -0.300* | 1.000 | |||||||
| Rperm*Rsai | 0.353* | 0.368* | 0.251* | 0.519* | 0.523* | 0.499* | 0.4405* | 0.274* | 0.438* | 0.277* | 1.000 | ||||||
| Rperm | 0.250* | 0.262* | 0.021 | 0.392* | 0.389* | 0.362* | 0.9935* | -0.323* | 0.997* | -0.318* | 0.424* | 1.000 | |||||
| Rsais | 0.277* | 0.277* | 0.318* | 0.503* | 0.499* | 0.436* | -0.3347* | 0.991* | -0.333* | 0.994* | 0.241* | -0.348* | 1.000 | ||||
| logSAU*logL | 0.428* | 0.432* | 0.984* | 0.497* | 0.504* | 0.529* | 0.0981* | 0.409* | 0.096* | 0.410* | 0.324* | 0.076* | 0.379* | 1.000 | |||
| logK*logSAU | 0.500* | 0.503* | 0.985* | 0.418* | 0.425* | 0.531* | 0.0856* | 0.374* | 0.076* | 0.362* | 0.292* | 0.059* | 0.336* | 0.984* | 1.000 | ||
| logSAU*Rperm | 0.312* | 0.322* | 0.350* | 0.433* | 0.435* | 0.426* | 0.8479* | -0.197* | 0.843* | -0.191* | 0.485* | 0.834* | -0.223* | 0.401* | 0.382* | 1.000 | |
| logSAU*Rsais | 0.334* | 0.339* | 0.646* | 0.544* | 0.547* | 0.497* | -0.2367* | 0.866* | -0.233* | 0.868* | 0.285* | -0.250* | 0.852* | 0.703* | 0.661* | -0.074* | 1.000 |
Conclusion du Chapitre 5
Ce chapitre empirique avait pour but d’éclairer les liens entre la structure du collectif de travail des exploitations et un des indicateurs de la performance de celles-ci, la productivité.
Par le biais de l’estimation d’une fonction de production de type Cobb-Douglas tenant compte de la composition du collectif de travail, nous avons mis en évidence que la structure du collectif de travail est un déterminant de la productivité des exploitations de fruits et légumes françaises. Les évolutions de la main-d’œuvre dans les exploitations peuvent donc influencer leur performance.
Nous montrons, d’autre part, que, dans ce secteur, le travail salarié est plus productif que le travail familial et, ce, même en contrôlant pour la différence saisonnière de la productivité marginale du travail en agriculture.
À la différence de ce que suggéraient les travaux empiriques précédents, le cantonnement des travailleurs salariés aux tâches saisonnières les plus productives n’explique donc pas l’inégale productivité entre la famille et le salariat.
La division des tâches et la spécialisation des travailleurs expliquerait la plus forte productivité des salariés [Allen et Lueck, 1998 ; Lambarraa et al., 2007 ; Lambarraa et al., 2009].
D’autre part, nos résultats indiquent que le travail salarié saisonnier est plus productif que le travail salarié permanent alors même que le capital humain spécifique des permanents et leur coût d’opportunité à être licenciés sont normalement plus élevés.
Ce résultat peut, bien sûr, s’expliquer par la spécialisation des travailleurs saisonniers sur des tâches marginalement très productives comme les travaux de récolte.
Pourtant, il suggère aussi de s’interroger plus avant quant aux formes d’emploi spécifiques que peut prendre le travail saisonnier dans le secteur des fruits et légumes.
En effet, la fidélisation de la main-d’œuvre saisonnière et le caractère extrêmement incitatif de certains contrats saisonniers pourrait aussi expliquer la différence de productivité.
 Vous pouvez télécharger ce travail de mémoire (en PDF ci-dessousfichier).
Vous pouvez télécharger ce travail de mémoire (en PDF ci-dessousfichier).