Traduction statistique : Canal bruité et Modèle de langue
Chapitre 2 :
Traduction statistique
En 1949, Warren Weaver a suggéré une approche de la traduction automatique basée sur les données statistiques. Cependant, les capacités limitées (en calcul et en mémoire) des ordinateurs de l’époque expliquent en grande partie que cette approche n’ait pas été poursuivie.
Sur l’effet de la révolution technique, la traduction statistique (Statistical Machine Translation SMT) est présentement une approche largement convoitée, bien qu’encore marginale dans le secteur industriel. Au début des années 90s, la traduction probabiliste a été ressuscitée par les chercheurs [Brown et al. 1993].
Dans ce chapitre, on explique le principe de la traduction statistique qui repose sur la métaphore du canal bruité. Nous décrivons les problèmes liés à la réalisation d’un système de traduction probabiliste, à savoir l’entraînement d’un modèle de transfert, d’un modèle de langue et le problème du décodage.
Nous décrivons sommairement les modèles de langue qui sont bien maîtrisés [Goodman et al., 2001] et à la fin de ce chapitre, nous étudions d’avantage les modèles de traduction probabiliste et en particulier les trois premiers modèles proposés par [Brown et al. 1993].
2.1 L’idée originale Shanon (canal bruité)
L’approche la plus courante de la traduction probabiliste s’inscrit dans le cadre des approches dites “canal bruité” (après les travaux de Shanon) qu’on explique ici de manière intuitive.
Deux personnes, un émetteur E et un récepteur R, souhaitent communiquer via un canal bruité. Ce canal est «tellement bruité» qu’une phrase S déposée par E à l’entrée du canal est reçue par R comme une autre phrase T, traduction de S.
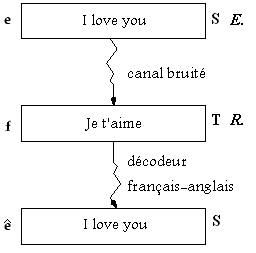
Figure 1: Illustration du canal bruité. L’anglais est ici le langage source du canal et le français le langage cible.
Le but pour R est de retrouver la phrase source à partir de la phrase reçue et ses connaissances du canal bruité. Chaque phrase de la langue source est une origine possible pour la phrase reçue T. On assigne une probabilité P(S|T) à chaque paire de phrases (S,T).
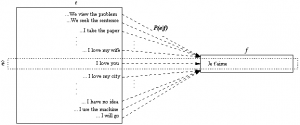
Figure 2: Chercher la phrase anglaise ê qui maximise la probabilité P(e|f).
On souhaite que le modèle du canal P(S|T) assigne une probabilité faible à des paires de phrases peu probables (exemple: We view the problem |Je t’aime) et une probabilité élevée à des paires plus probables (Je t’aime | I love you).
Dans ce travail, nous traduisons de la langue française vers la langue anglaise. Il est important de bien réaliser que dans le cadre de l’approche du canal bruité, la langue source est celle de l’émetteur et la langue cible est celle de récepteur.
Lorsqu’on considère le décodeur, c’est le contraire. Cette distinction est souvent à l’origine de confusion dans la littérature, aussi prenons-nous la convention suivante dans ce mémoire.
Convention: Nous prenons pour langue source (S) l’anglais et pour cible le français (T). On désigne par source l’entrée du canal bruité et cible la sortie du canal bruité ceci évite l’ambiguïté des termes source/cible dans l’approche du canal. (Voir figure 1).
Le problème général de la traduction statistique est de trouver la phrase ê, étant donnée une phrase fJ, qui maximise P(eI|fJ). De manière plus formelle :
![]() . (2.1)
. (2.1)
D’après le théorème de Bayes:
![]() (2.2)
(2.2)
Comme le dénominateur de l’équation (2.2) est indépendant de eI, l’opération de maximisation devient alors:
![]() (2.3)
(2.3)
On appelle P(eI), un modèle de langue source, tandis que le deuxième facteur P(fJ|eI) est appelé un modèle de traduction.
Alors, le problème de la traduction se divise en trois sous problèmes que nous décrivons par la suite :
Calculer les paramètres du modèle de langue;
Calculer les paramètres du modèle de traduction;
Réaliser un décodeur, c’est-à-dire un mécanisme capable d’effectuer l’opération de maximisation de l’équation (2.3) en un temps acceptable.
2.2 Le modèle de langue
Un modèle de langue est un modèle qui spécifie une distribution P(e) sur les chaînes ei de la langue modélisée:
![]()
Sans perte d’information, si l’on considère que eI est une suite de I mots (une phrase de I mots), e1 = w1 … wI , alors:
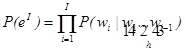 (2.4)
(2.4)
Où h est appelée l’historique.
Un modèle de langue probabiliste peut être présenté comme une fonction donnant la probabilité d’observer un mot étant donné ceux déjà observés. Cette approche a déjà montré son utilité dans plusieurs applications dont la reconnaissance de la parole et de caractères ou encore la correction de fautes d’orthographe.
L’estimation des distributions P(w|h) où w est un mot et h l’historique (l’ensemble des mots déjà vus) est un problème complexe (trop de paramètres à estimer) que l’on simplifie habituellement de la manière suivante:
![]()
La probabilité d’un mot est conditionnée «seulement» par les deux derniers mots dans l’historique de w. Cette simplification est appelée un modèle trigramme.
Nous utilisons dans notre travail un modèle de langue développé par le RALI sur un corpus de plus d’un million de phrases en anglais extraites du HANSARD. Pour plus d’information on peut consulter le travail de [Goodman et al, 2001].
Le modèle de langue est nécessaire pour que le modèle de traduction puisse concentrer ses masses de probabilités sur des paires de phrases à peu près raisonnables. Soit f J une phrase connue donc bien formée, eI l’est à peu près, grâce au modèle de langue.

