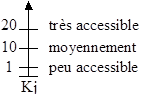2. L’analyse multicritère
Il y a tout juste 30 ans, la méthode ELECTRE venait apporter une solution aux problèmes rencontrés par les analyses coûts-avantages. Ces dernières reposent en gros, comme nous l’avons vu, sur le même principe : avantages et coûts sont évalués sur des critères mesurables et assortis, en outre, de la même unité de mesure (l’unité monétaire).
La commensurabilité des critères d’évaluation facilite leur agrégation au sein d’une fonction qui peut être considérée comme une sorte de critère décisionnel synthétique qu’il convient d’optimiser pour obtenir un préordre total sur l’ensemble des projets considérés. Mais nous savons que la nature non marchande de certains critères d’évaluation limite grandement la portée pratique de la démarche.
Avec la méthode ELECTRE, le recours à l’étalon monétaire n’est plus indispensable ; les évaluations ne sont pas obligatoirement des mesures, mais de simples ordres de grandeur servant à comparer les projets sur chaque critère. L’incommensurabilité des critères interdisant la voie de l’agrégation complète, l’exploitation de ces comparaisons ne vise plus à ranger les différents projets par ordre de préférence décroissante, mais à éliminer les « moins bons » pour arriver progressivement à une solution acceptable, à un bon compromis parmi des projets difficilement comparables.
La voie suivie par ELECTRE est donc simple, mais paradoxalement on constate que l’analyse multicritère est moins appliquée que les analyses dérivant du calcul économique public. L’évaluation a priori des politiques structurelles constitue, par exemple, un domaine largement ouvert à la démarche multicritère, mais les travaux réalisés relèvent, pour la plupart, de l’analyse coûts-avantages.
La remise en cause du paradigme de l’optimisation sur laquelle débouche la démarche multicritère est sans doute à l’origine de ce paradoxe. En acceptant l’incomparabilité et l’intransitivité comme des situations ordinaires, la relation de surclassement multicritère ne garantit plus la rationalité du choix et de l’optimalité de la solution qui s’en dégage.
Les résultats proposés au terme d’une analyse multicritère ne sont pas toujours aussi nets que ceux proposés par les méthodes optimisantes du calcul économique néoclassique. D’où l’impression de complexité qui se dégage généralement de l’analyse multicritère (Benard, 1985). Ajoutons que cette dernière a beaucoup évolué au cours de ces trente dernières années et que cette évolution ne s’est pas toujours déroulée dans le sens de la transparence.
2.1. Les concepts de base de l’AMD
2.1.1.Points de vue, critères
Désignons par I={1…i…n} l’ensemble des actions possibles, par exemple tous les lieux d’un territoire susceptibles d’être retenus comme site d’implantation pour une entreprise donnée, et par J={1…j…m} la liste des points de vue pris en compte par le décideur. La notion de point de vue est couramment confondue avec celle de critère. Il nous faut cependant distinguer les deux notions.
Un point de vue j est un axe de signification particulier que retient le décideur afin de porter un jugement sur chaque action de I. Dans un problème de localisation, l’accessibilité à la demande potentielle est un point de vue important.
L’accessibilité d’un site sera plus ou moins importante selon la position qu’il occupe dans la surface de la demande ; les lieux excentrés par rapport aux points de concentration de la demande seront, selon ce point de vue, défavorisés par rapport aux lieux plus centraux. Pour conforter ces jugements d’une manière plus précise, on fait intervenir la notion de critère.
Un critère est un procédé qui permet de comparer les actions selon un point de vue donné. Les comparaisons s’effectuent sur une base numérique, d’où la définition formelle : le critère associé au point de vue j est l’application, notée gj, de I dans le corps des réels :
1.(1)gj:I R
i gj(i)
Le nombre gj(i) représente l’évaluation de l’action i sur le critère gj. Dans ce qui suit, nous supposerons à titre de simplification que le sens de la préférence est croissante sur chaque critère gj : l’action i est jugée d’autant plus favorablement que la valeur gj(i) est grande.
2.1.2. Pouvoir de discrimination d’un critère
La manière dont s’effectue la comparaison des actions sur chaque critère dépend du pouvoir de discrimination de celui-ci (Vincke, 1980 ; Roy, 1985 ; Roy et Vincke, 1987). Lorsque le pouvoir de discrimination de gj est parfait, on dit que gj est un vrai-critère. Mais si gj possède un pouvoir de discrimination imparfait, il s’agira d’un quasi-critère ou d’un pseudo-critère.
Vrai-critère.
Etant donné deux actions quelconques i et i’, une relation de préférence stricte Pj restreinte au critère gj, et une relation d’indifférence Ij restreinte au même critère, on a :
gj(i) – gj(i’) > 0i Pj i’
1.(2)gj(i) – gj(i’) = 0i Ij i’ et i’ Ij i
gj(i) – gj(i’) < 0i’ Pj i
gj est un vrai-critère, son pouvoir de discrimination est parfait : une faible différence, aussi minime soit-elle, fait basculer la situation d’indifférence dans une situation de préférence stricte. Il ne peut y avoir indifférence entre i et i’ (sur le critère gj) que si gj(i)=gj(i’). Toute différence positive gj(i)-gj(i’) révèle une préférence stricte (par rapport au critère gj) en faveur de i.
Avec un vrai-critère, on ne peut que discriminer sans nuance des situations d’indifférence et des situations de préférence stricte et rejeter toute situation de préférence faible. C’est pour cette raison que l’on dira qu’un vrai-critère possède un pouvoir discriminant absolu.
Cette légitime réticence à admettre que le moindre écart, si petit soit-il, entre gj(i) et gj(i’) conduit à établir une relation de préférence stricte entre i et i’ entraîne alors l’évaluateur à considérer des formes de critères qui ne sont plus de vrais critères et dont nous dirons qu’ils possèdent un pouvoir discriminant non absolu ou nuancé.
« Le pouvoir discriminant d’une fonction-critère g se rapporte à la faculté plus ou moins marquée que l’homme d’étude lui reconnaît pour discriminer des situations de préférence stricte, d’indifférence et de préférence faible sur la base d’une plus ou moins grande importance de la différence gj(i)-gj(i’) » (Roy, 1985).
Ainsi, lorsque l’homme d’étude, estime nécessaire d’opter pour un pouvoir discriminant plus nuancé, il peut le faire de façon simple en faisant intervenir un ou deux seuils, dits seuils de discrimination, comme nous allons le voir.
Quasi-critère
On admet donc à présent qu’une légère différence entre deux évaluations peut-être compatible avec une situation d’indifférence. A cet effet, on considère un nombre positif, noté qj et appelé seuil d’indifférence. Avec les mêmes notations que précédemment, la comparaison des actions sur gj s’effectue de la manière suivante :
gj(i) – gj(i’) > qji Pj i’
1.(3) -qj gj(i) – gj(i’) qji Ij i’ et i’ Ij i
gj(i) – gj(i’) < -qji’ Pj i
Le pouvoir de discrimination de gj est imparfait dans la mesure où la situation d’indifférence est associée non plus à un point (valeur 0), mais à un intervalle [-qj , qj]. Dans ce cas, on dit que gj est un quasi-critère.
Pseudo-critère.
Dans le cas précédent, le passage de l’indifférence à la préférence stricte s’effectue sur la base d’un seuil fixé d’une manière précise : une différence gj(i)-gj(i’) tout juste plus grande que qj conduit directement de i Ij i’ à i Pj i’. Pour nuancer la transition entre I et P, on introduit une zone intermédiaire appelée préférence faible et notée Q. A cet effet, on considère un nombre positif pj>qj, appelé seuil de préférence. 1.(3) devient :
gj(i) – gj(i’) > pji Pj i’
qj <gj(i) – gj(i’) pji Qj i’
1.(4)-qj gj(i) – gj(i’) qji Ij i’ et i’ Ij i
-pj gj(i) – gj(i’) < -qji’ Qj i
gj(i) – gj(i’) < -pji’ Pj i
Le critère gj est un pseudo-critère.
Pondération
Une pondération définie sur J reflète les préférences du décideur quant au rôle tenu par chaque point de vue dans le problème décisionnel. Formellement, il s’agit d’une application, notée p, de J vers l’ensemble des nombres entiers positifs :
1.(5)p :J N
j p(j)
Le nombre p(j) représente le poids (absolu) du critère gj (ou du point de vue j). On notera que la pondération permet de comparer les points de vue selon un procédé analogue à celui du vrai-critère. En effet, introduisons dans J une relation de préférence stricte P et une relation d’indifférence I. Alors :
p(j) – p(j’) > 0j P j’
1.(6)p(j) – p(j’) = 0j I j’ et j’I j
p(j) – p(j’) < 0j’ P j
Le pouvoir de discrimination de la pondération est donc supposé parfait. Cette hypothèse est peu réaliste, mais dans les applications on peut toujours procéder à des analyses de sensibilité en faisant varier légèrement la valeur des poids. Par la suite, nous utiliserons les poids relatifs :
(j) = p(j) / [p(j) ; j = 1…m], de telle manière que [(j) ; j = 1…m] = 1.
2.1.3. Démarche évaluative de l’A.M.D
On entend par démarche évaluative la manière dont on construit un critère gj.
Nous avons en effet proposé une définition très générale de la notion de critère (relation 1.(1).) puisqu’elle nous dit seulement qu’un critère est un modèle quantitatif : des valeurs sont associées aux diverses actions dans le but de comparer ces dernières. Il nous faut rentrer dans le détail du modèle pour savoir comment de telles valeurs sont obtenues.
La construction de critères s’effectue selon deux types de procédés : le premier, assez rapide, utilise des échelles d’appréciation, le second, nettement plus sophistiqué, recours à la définition de fonctions numériques. Fustier (2000) illustre ces procédés par la construction du critère « accessibilité au marché de consommation ».
La technique des échelles d’appréciation.
A chaque point de vue j, on associe une échelle numérique Kj, discrète ou continue, dont les échelons servent à apprécier le degré d’adéquation des actions au point de vue correspondant. Le premier échelon correspondant à la valeur inf Kj signifie une faible adéquation (voire une absence totale d’adéquation) avec le point de vue considéré ; au contraire, la valeur sup Kj associée au dernier échelon rend compte d’une très forte adéquation. La hauteur de Kj est définie par hj = sup Kj – inf Kj.
Le critère gj fait correspondre à toute action de I, un (unique) échelon de Kj. L’établissement d’une telle correspondance est le fait de l’évaluateur qui agit en fonction de sa connaissance du terrain et des statistiques disponibles (pour l’accessibilité d’un site, il est opportun de disposer de renseignements concernant la population environnante, l’état des réseaux de communication etc.).
La manière dont on devra comparer les actions dépend de la plus ou moins grande finesse de l’échelle. Une échelle discrète comportant un nombre peu élevé d’échelons est compatible avec le modèle du vrai-critère. Par exemple :
Figure 1. Exemple d’échelle discrète.
Cette échelle offre peu de possibilité pour définir une plage d’indifférence et une zone de préférence faible. Mais lorsque l’échelle est plus fine et, a fortiori continue, les modèles du quasi-critère et du pseudo-critère s’imposent naturellement, car la correspondance entre I et Kj, même si elle repose sur des bases solides, comporte néanmoins une dose de subjectivité qui interdit de considérer les gj(i) comme des grandeurs exactes.
Définition de fonctions-critères.
Une conception plus « scientifique » de la démarche évaluative consiste à définir gj par une fonction à valeurs réelles. On se doute de la difficulté de la démarche, en particulier lorsqu’il s’agit d’exprimer par une structure mathématique des points de vue qualitatifs. Il n’y a pas de règle en la matière, la construction d’une « bonne » fonction relève plus de l’art que de la science.
S’agissant d’évaluer l’accessibilité d’un site i au marché de consommation, on peut songer au potentiel de population et poser :
2.(1.)gj(i) = b [c(i’)/d(i,i’) ; i’ = 1…i…n]
avec :
b : constante de proportionnalité
c(i’) : population de la zone i’
d(i,i’) : distance entre les zones i et i’ : exposant de d ayant pour effet d’atténuer (lorsque <1) ou d’accentuer (>1) l’effet de friction provoqué par la distance.
Observons que (dans 2.(1).) la somme est étendue de l’indice 1 à n en passant par i, ce qui signifie que la distance d(i,i) doit être non-nulle. Pour estimer la distance intra-zone du site i, certains auteurs font l’hypothèse que chaque zone i est de forme circulaire. Connaissant la superficie s(i) de la zone i, on a s(i)=r2 et r= [s(i)/ ]½. Sachant que la distance moyenne par rapport au centre d’un cercle est égale à la moitié du rayon, on pose :
2.(2)d(i,i)=½[s(i)/ ]½.
Ce type de fonction-potentiel a été utilisé dans les années 50 comme critère (unique) de localisation de l’unité de production et plus récemment, a donné d’assez bons résultats en matière de localisation commerciale ou encore de localisation des services publics. Mais souffrant d’une trop forte analogie avec les lois de la mécanique classique, l’approche « gravitationnelle » de l’analyse de la localisation n’a pas été un franc succès en économie spatiale.
En effet, rien n’est dit sur la valeur que doit prendre l’exposant de la distance dans chaque application particulière de la formule du potentiel, il en est de même pour l’unité de distance (le coût de transport est-il préférable au temps de transport ?) et l’unité de masse (la population est-elle un bon reflet du marché ?).
On aura compris que le potentiel de population caractérisant un site de localisation possible est un indicateur et seulement un indicateur de sa plus ou moins grande proximité par rapport au marché régional. Les évaluations qui sont données par la fonction-potentiel sont entachées d’imprécision. La fonction-potentiel comme toute autre fonction-critère relève du modèle pseudo-critère.
Les limites du pseudo-critère.
Le passage de la notion de point de vue à celle de critère est une phase délicate qui conditionne dans une certaine mesure le résultat du problème décisionnel. La tendance actuelle qui consiste à utiliser des fonctions-critères à seuils va dans le sens d’une plus grande opacité de l’AMD.
L’expression numérique d’un point de vue, énoncé le plus souvent d’une manière verbale par le décideur, ne relève pas d’une procédure bien définie, mais repose sur la capacité de l’homme d’études à exhiber une relation fonctionnelle qui ne trahisse pas l’axe de signification révélé par le décideur.
Lorsque l’on exprime le point de vue « accessibilité » par une fonction-potentiel du type 2.(1), on opère un premier choix, le plus souvent guidé par la simplicité de la structure, parmi un ensemble de fonctions susceptibles de répondre au problème.
Puis lorsque l’on fixe des valeurs aux paramètres de la fonction et que l’on assigne des unités de mesure aux variables, on opère d’autres choix tout aussi discutables que le premier. Heureusement, les seuils de discrimination sont là pour nous rappeler que les évaluations produites par les fonctions-critères ne sont pas des données exactes, mais de simples ordres de grandeur qu’il faut manipuler avec prudence. Mais comment fixer la valeur de ces seuils ?
Là encore, aucune réponse nette ne peut être donnée : tout dépend de la fonction considérée. S’agissant, par exemple, de comparer des projets en fonction (inverse) du niveau sonore qu’ils procurent (ROGERS et BRUEN 1997), des études de perception permettent de déterminer avec une certaine précision les nombres de décibels correspondants aux seuils d’indifférence, de préférence et de veto.
Mais si l’on se réfère une nouvelle fois à la fonction-potentiel, on se rend compte que la détermination d’un seuil de discrimination particulier, exprimé dans une unité de mesure aussi peu parlante que le nombre d’habitants par unité de distance, est un choix hautement hasardeux. Pour éviter cet abus de précision, on pourrait définir les seuils de discrimination de manière non ponctuelle, en les formalisant par exemple par des nombres flous (MFOUKA 1993), mais cette procédure conceptuellement intéressante risquerait de compliquer les choses et de provoquer un rejet des méthodes d’AMD qui, en l’état actuel, sont déjà assez lourdes à manier.
Si la volonté de sauvegarder les nuances s’accompagne d’une plus grande complexité méthodologique, peut on dire que les résultats s’en trouvent améliorés?
En mettant davantage l’accent sur la phase d’évaluation proprement dite que sur le stade final de la prise de décision, l’analyse multicritère est devenue une « aide multicritère à la décision » (AMD) avec, cependant, une conception bien particulière de la démarche évaluative. Celle-ci vise essentiellement à construire des fonctions numériques qui serviront à comparer les actions selon les différents points de vue retenus dans le problème de décision.
L’expression mathématique d’un axe de signification particulier est une tâche difficile qui repose exclusivement sur le savoir-faire de l’évaluateur. Il ne faudra donc pas considérer les évaluations comme des données exactes ; une légère différence entre deux évaluations peut être tolérée et ne remet pas en cause la situation d’indifférence.
Mais à partir de quel moment cette différence devient-elle significative ? Quand peut-on dire qu’une action est préférée « faiblement » ou « nettement » à une autre ? Pour traiter ces nuances, les nouvelles méthodes d’AMD introduisent des seuils dont les valeurs sont laissées à l’appréciation de l’utilisateur.
C’est justement là où réside le problème, car la prise de décision dépend moins de la logique interne de la méthode que d’un ensemble de valeurs subjectivement décidées a priori. Les nouvelles méthodes d’AMD sont donc difficiles à juger, ce qui n’incite guère les décideurs potentiels à les utiliser.
Il est difficile de porter un jugement sur les nouvelles méthodes. La simple variation des seuils de discrimination des pseudo-critères aura pour conséquence d’engendrer des résultats plus proches ou au contraire plus dissemblants.
N’étant pas en mesure de porter un jugement sur la validité des seuils de discrimination, il en va de même pour les résultats qui en découlent.
Finalement, on s’aperçoit que l’évaluation est loin d’être une science exacte, il n’existe aucune formule mathématique permettant de mesurer le degré d’accessibilité et encore moins de beauté d’un paysage.
Ce que l’on peut faire au mieux c’est évaluer subjectivement ces notions puisque les seuils utilisés dans les méthodes exposées précédemment sont eux-même fixés de manière discutable. Il nous semble alors tout aussi légitime de nous en tenir à l’appréciation d’experts qui fourniraient des évaluations (en connaissance de cause), puis, de tenter de les rendre moins subjectives en effectuant une synthèse des évaluations partielles des experts conduisant à une évaluation globale.
Cette manière de construire un critère a déjà fait l’objet de travaux, nous en présentons ici les principaux développements.