Modélisation – Partie II Introduction Cette partie est relative à la modélisation; l’objectif est présenter de façon concise mais mathématiquement complète des modèles nous permettant de confirmer ou d’infirmer les hypothèses émises quant à la contribution des TIC dans la croissance économique, leur évolution et les déterminants de leur évolution. Pour ce faire nous disposons d’un échantillon de données annuelles de la période 1980 à 2008. L’objectif du modèle statistique est d’approcher au mieux les caractéristiques du modèle réel. L’approche inférentielle et confirmatoire permet de valider ou infirmer les hypothèses formulées a priori ou après la phase exploratoire, et d’extrapoler certaines propriétés de l’échantillon à une population plus large. Les hypothèses sont validées par l’utilisation de tests statistiques ou de modèles probabilistes. Ce type d’analyse faitappel aux méthodes explicatives et prévisionnelles. Chap. I Etude empirique de l’impact du secteur TIC sur la croissance économique Modèle de régression linéaire multiple. I. Présentation théorique du modèle La régression multiple est définie comme un outil permettant d’étudier et de mesurer la relation existant entre une variable (Y), dite variable expliquée, et d’autres variables, dites variables explicatives. Effectuer une régression multiple consiste à se baser sur les données d’un échantillon afin de déterminer une estimation de la relation mathématique entre la variable expliquée et les variables explicatives. Etant donné un échantillon, t= 1,…, n on cherche à expliquer, avec le plus de précision possible, les valeurs prises par Y, dite variable endogène, à partir d’une série de variables explicatives . Le modèle théorique, formulé en termes de variables aléatoires, prend la forme suivante : t=1, …, n
Où est l’erreur du modèle qui exprime, ou résume, l’information manquante dans l’explication linéaire des valeurs de à partir des (problème de spécifications, variables non prises en compte, etc.). sont les paramètres à estimer. De façon matricielle, ce modèle peut s’écrire de la façon suivante. Soit de la manière compacte, Avec : · Y est de dimension (n, 1) · X est de dimension (n, k + 1) · â est de dimension (k+1, 1) · å est de dimension (n, 1) · la première colonne sert à indiquer que nous procédons à une régression avec constante. Les résultats d’une régression multiple sont donnés d’une part à travers l’équation de régression qui détermine la relation entre la variable expliquée et les variables explicatives, et d’autre part à travers divers coefficients et graphiques qu’il s’agira d’analyser afin: · d’établir le degré de fiabilité de l’estimation ; · d’examiner la significativité des résultats ; · d’examiner si la relation entre la variable expliquée et chaque variable explicative est réelle ou seulement apparente. La régression multiple peut faire l’objet de différents usages selon les attentes. Elle peut être utilisée afin de décrire des relations entre les variables explicatives et d’analyser leur action sur la variable expliquée, afin de faire des estimations ou des prédictions, ou bien même afin de pouvoir utiliser l’équation de régression comme un outil de contrôle (si vous souhaitez par exemple savoir de quelle manière modifier la valeur d’une variable explicative afin d’obtenir une valeur fixée de Y). I.1. Diagramme de dispersion Le nuage de points ou diagramme de dispersion est la représentation graphique dans le plan cartésien de l’ensemble des paires de données. Ces données proviennent d’une série statistique de variables obtenues à partir d’une étude menée sur un échantillon ou sur une population. Une fois la représentation graphique effectuée, il est facile de soupçonner l’existence d’une certaine relation entre les variables deux à deux (caractères étudiés). Il faut maintenant chercher à exprimer cette relation à l’aide d’une équation mathématique Ce constat pourrait être est confirmé par le tableau des corrélations. I.2. Estimation des paramètres Il existe plusieurs méthodes permettant d’estimer le modèle théorique par le modèle empirique ; il s’agit entre autres de la méthode des moindres carrés et de la méthode de la vraisemblance. La méthode habituellement utilisée est celle des moindre carrés que nous allons également adopter. Cette méthode essaie de construire une droite de régression empirique qui minimise la somme des carrés des distances verticales entre cette droite et chacun des points observés. On appelle résidu ou erreur empirique ou écart de prévision, la valeur , soit la différence (l’écart vertical) entre la valeur observée yi de Y et la valeur estimée obtenue à partir de la droite de régression, lorsque x= xi. À travers cette méthode, on recherche minimisant I.3. Validation du modèle I.3.1. Test statistique sur les coefficients du modèle La liaison globale entre Y et est-elle significative ? Modèle Test H0 = … = = 0 (Y = + ne dépend pas des X) H1 Au moins un j 0 (Y dépend d’au moins un X) Statistique utilisée Décision de rejeter H0 au risque de se tromper Rejet de H0 si F ; étant le Fractile d’une loi de Fisher-Snedecor. L’apport marginal de est-il significatif ? Modèle Test H0 j = 0 (On peut supprimer) H1 j 0 (Il faut conserver) Statistique utilisée Décision de rejeter H0 au risque de se tromper Rejet de H0 si ; le Fractile d’une loi de Student. I.3.2. Etude de la colinéarité Le problème de multicolinéarité produit une instabilité des coefficients estimés. Elle peut être à la source d’une non significativité de certaines variables qui sont en réalité significatives. En cas de multicolinéarité parfaite, l’estimation des coefficients est même parfois impossible. Il convient dès lors de s’assurer que cette contrainte ne se pose pas dans le cas d’espèce. Pour y arriver, nous mettons en oeuvre un test de détection de la présence de multicolinéarité. Le test retenu est celui de Farrar D.E. et Glauber R.R. (1967). Le principe de ce test est le suivant La première étape de ce test consiste à calculer la matrice des coefficients de corrélation entre les variables explicatives. ï On calcule le déterminant D de la matrice des coefficients de corrélation entre les variables explicatives du modèle. ïTest D = 1 (les séries sont orthogonales) Vs: D < 1 (les séries sont dépendantes) ï Statistique avec ï Si lu dans la table à ddl et au seuil á choisi rejet de il y a présomption de colinéarité. ï on accepte l’hypothèse d’orthogonalité. On peut également mesurer la multicolinéarité avec d’autres critères comme la tolérance et le VIF. Mesure de la multi-colinéarité Tolérance et VIF ï Tolérance = 1 – (; Autres X) ; Il est préférable d’observer une tolérance supérieure à 0.33. ï VIF = Variance Inflation Factor = 1 / Tolérance ; Il est préférable d’observer un VIF inférieur à 3. ï est la somme des carrés expliquée par les variables . F partiel ï On obtient un petit si est petite ou bien R2 ( ; Autres variables X) est grande. I.3.3. Coefficient de détermination R2 Il existe trois mesures possibles pour quantifier l’intensité de la relation entre X et Y: le coefficient de détermination de Y en fonction de X, le coefficient de corrélation entre X et Y, la covariance entre X et Y. Le coefficient de détermination théorique de Y en fonction de X, noté mesure la proportion de la variation de Y qui est expliquée par la régression ou qui est expliquée par la variable X au niveau de toute la population Le coefficient de détermination indique si le modèle linéaire défini colle aux données. En pratique est inconnu, car on ne possède pas d’information sur toute la population mais seulement sur un échantillon de taille n, alors on estimera à partir de l’échantillon. A travers la formule de décomposition suivante Cette estimation nous donne Cette qualité de l’ajustement et l’appréciation que l’on a du doivent être tempérées par le degré de liberté de l’estimation. En effet, lorsque le degré de liberté est faible, il convient de corriger le a fin de tenir compte du relativement faible nombre d’observations comparé au nombre d’observations de facteurs explicatifs par le calcul d’un corrigé noté I.3.4. Vérification des hypothèses du modèle Avant une régression, plusieurs hypothèses sont en général émises et il convient de vérifier si ces hypothèses sont respectées à la fin de l’étude. Ces hypothèses principalement liées au terme d’erreur sont ï L’erreur est une variable aléatoire d’espérance 0 ï La variance de , dénotée ou , est la même pour toutes les valeurs de X ; homoscedasticité des erreurs (variance constante) ; ï Les valeurs desont indépendantes ; pas d’autocorrélation des erreurs. ï L’erreur est distribuée selon une loi normale . I.3.5. Prévision de la variable dépendante connaissant les variables explicatives Intervalle de prévision de Modèle = future valeur de = prévision de Intervalle de prévision de yi au niveau 0.95 Formule simplifiée; nous aurons ainsi une observation i qui sera mal reconstituée par le modèle si n’appartient pas à son propre intervalle de prévision. II. Mise en pratique du modèle Etude empirique de l’impact du secteur TIC sur la croissance économique Les études empiriques ayant pour objet d’évaluer l’impact des TIC sur la croissance économique se sont pour la plupart heurtées à des problèmes de définition et de mesure. Deux raisons principales expliquent cette difficulté d’une part, le secteur des TIC présente des frontières floues, spécialement en ce qui concerne le domaine des télécommunications où l’éventail des produits et des services est important ; d’autre part, les résultats obtenus par les économètres varient en fonction des statistiques disponibles et des techniques économétriques utilisées. Dans les travaux empiriques, la définition du secteur a été souvent limitée aux sous-secteurs de l’informatique et/ou des télécommunications. Cette restriction est essentiellement due au manque de statistiques fiables sur une longue période. Nous nous bornerons dans notre étude au seul secteur des télécommunications compte tenu du manque des statistiques fiables sur le secteur de l’électronique et de l’informatique. En supposant que la valeur ajouté du secteur TIC, peut être considérée comme équivalente à la valeur ajouté du secteur des télécommunications, nous pouvons déjà analyser l’évolution du secteur. Tableau 11: Part de la valeur ajouté de l’agriculture, de l’industrie, des secteurs TIC et hors TIC dans le PIB Marocain (%)
| Année | VA_Agri/PIB | VA_Ind/PIB | VA_HTIC/PIB | VA_TIC/PIB |
| 1980 | 18,43 | 16.83 | 43,04 | 1,3 |
| 1990 | 17,73 | 18,44 | 41,47 | 2,02 |
| 2000 | 13,83 | 17,57 | 44,12 | 2,28 |
| 2008 | 15,48 | 16,45 | 40,93 | 3,57 |
Année VA_Agri/PIB VA_Ind/PIB VA_HTIC/PIB VA_TIC/PIB
On peut constater à l’aide du tableau ci-dessus que le poids de l’économie de l’information est faible, mais croît au cours des 30 dernières années au Maroc. La part de ce secteur a presque triplé pendant cette période, elle est en effet passée de 1,3 % à 3,57 % du PIB en 2008, par contre dans d’autres secteurs on constate une variation plus ou moins modérée de leur contribution en pourcentage du PIB. Tableau 12 Part et croissance des investissements et de la valeur ajoutée du secteur TIC.
| Année | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| FBCF_TIC/FBCF_Total | 2.83 | 2.76 | 2.80 | 2.79 | 2.78 | 2.77 |
| VA_TIC/PIB | 3.29 | 3.47 | 3.76 | 3.83 | 3.58 | 3.57 |
| CVPIB | – | 6.54 | 7.51 | 4.71 | 0.43 | 3.44 |
Année 2003, 2004, 2005, 2006, 2007, 2008 FBCF_TIC/FBCF_Total VA_TIC/PIB CVPIB
On constate que pendant la période allant de 2003 à 2008, la part du secteur TIC dans le PIB est en moyenne de 2,98% annuellement , cette valeur a plus que doubler par rapport a la contribution de la valeur ajouté du secteur dans le PIB dans les année 1980, malgré une augmentation conséquente du PIB de 7,74 % en moyenne par an. Ceci a été rendu possible en raison d’une croissance rapide de 9,93 % de la valeur ajoutée du secteur des TIC. Durant la même période, l’évolution de la contribution du secteur des TIC à la variation du PIB (notée CVPIB), estimée par le rapport ?VATIC/?PIB, a été très fluctuante pendant la même période ; ce qui ne permet pas en effet d’avoir une idée précise sur la contribution réelle du secteur, d’où l’intérêt d’une illustration économétrique. II.1. Les variables d’analyse D’un point de vue méthodologique, nous avons choisi d’évaluer la contribution du secteur des TIC à la croissance économique au Maroc à partir du modèle de Solow qui s’appuie sur la fonction de production (ou technologie) de type Cobb Douglass homogène à progrès technique neutre11(*) Y=F(A,K, L)=AKaLß.Dans cette expression A représente la productivité globale des facteurs dont la variation relative (le progrès technique) représente la partie de la croissance de la production non expliquée par les montants de capital et de travail. Les coefficients á et â représentent respectivement les élasticités de production du travail, et du capital. Pour une entreprise qui cherche à réduire au minimum les coûts et dans des conditions de concurrence sur les marchés des facteurs, ces coefficients correspondent aux parts respectives des différents facteurs de production dans les coûts. Toutefois, afin d’évaluer la contribution du secteur des TIC, nous avons décomposé le stock de capital en deux parties selon qu’il s’agisse du secteur des TIC (KTIC) ou non (KHTIC). Cette distinction est adoptée dans la littérature économique consacrée (Jorgenson et Stiroh, 2000 ; Jorgenson, 2001 ; Gilles et L’Horty, 2003). La variable KTIC peut faire apparaître une élasticité spécifique et se caractérise en général par des taux de dépréciation du capital différents et par des salaires qui sont, dans le domaine des TIC, plus élevés que dans les autres secteurs. L’absence de données statistiques sur les investissements dans le secteur TIC pour toute la période de notre étude (1980 à 2008) nous amène à limiter notre étude à l’examen du secteur des télécommunications comme indicateur de l’évolution du stock de capital dans le secteur des TIC. Ainsi, nous avons supposé que le stock de capital en télécommunications pour l’année 1980 est égal à la formation brute de capital fixe (FBCF)12(*) dans ce secteur fourni par les comptes nationaux. Par conséquent, la détermination du stock de capital pour la période 1980-2008 a été évaluée en faisant l’hypothèse que Kt+1= (1-ä) Kt + FBCFt+1 où ä représente le taux de dépréciation du stock de capital. Dans le secteur des télécommunications, il est généralement admis que ce taux est proche de 1/8, tandis que pour le reste des secteurs nous avons retenu le taux habituel de 8 %. Pour le reste des secteurs la même démarche a été adoptée, leur FBCF ayant été obtenue en déduisant la FBCF du secteur TIC de la FBCF totale nationale. La variable Y représente le PIB total calculé aux prix de 1980. Il est donné par les Comptes de la Nation publiés par la DCN (Direction de la Comptabilité Nationale de Rabat). Pour l’emploi L, cette variable décrit la quantité d’effort fournie par les employés dans le processus de production et pour laquelle, ils sont embauchés et rémunérés. Face à l’impossibilité de quantifier cet effort, plusieurs estimations sont procédées, soit par: – Le nombre d’employés contribuant directement ou indirectement dans le processus de production, en se justifiant, du fait que cet effort est fourni par eux donc il en sera fortement corrélé. Or le problème qui se pose est la négligence du niveau de qualification des travailleurs, de l’intensité de cet effort, et de la pénibilité du travail. – Le nombre d’heures de travail en plus des problèmes posés au dessus, ces heures ne peuvent être en général que celles de présence, ou celles payées et non celles effectivement oeuvrées. Mais malgré qu’elle constitue une base imparfaite (comme tous les auteurs le reconnaissent) la deuxième est la plus utilisée, avec quelque fois des améliorations, en essayant de résoudre les problèmes posés surtout celui de la qualification, en procédant par la pondération des heures travaillées par leurs coûts (toute charge comprise). Pour notre cas, pour des raisons d’absence de données plus précises nous nous limitons, à la première méthode c’est-à-dire à la population active occupée en nous référant aux enquêtes nationales emplois et en complétant certaines années par rétropolation. II.2. Formulation du modèle Une fois les variables identifiées, le modèle de la fonction de production pourrait se présenter sous la forme suivante En introduisant la fonction logarithme pour linéariser le modèle, on obtient l’expression suivante Avec la variable KTIC qui représente le stock de capital du secteur TIC, la variable KHTIC, représente le stock de capital du secteur hors TIC, la variable Y représente le PIB total calculé au Prix de 1980 et la variable L qui représente le stock de travail engagé à l’échelle nationale ou encore la population active occupée opérant sur le territoire Marocain. II.3. Présentation du diagramme de dispersion Figure 10 Présentation du diagramme de dispersion entre variables. Le graphique présentant les diagrammes de dispersion des variables deux à deux, laisse entrevoir l’existence d’une relation linéaire entre le Ln_PIB et les autres variables Ln_KTIC, LnKHTIC et Ln_L. Ces résultats suggèrent un modèle de régression linéaire multiple expliquant le PIB en fonctions des trois variables explicatives. II.4. Estimation des paramètres du modèle L’application de la méthode des moindres carrés ordinaires nous a permis d’obtenir les résultats suivants Tableau 12 Tableau des coefficients du modèle avant introduction de la variable Dummy.
| Tableau des coefficients du modèle | |||||||
| Modèle | Coefficients non standardisés | Coefficients standardisés | t | Sig. | |||
| B | Erreur standard | Bêta | |||||
| (Constante) | 6,870 | ,255 | 26,968 | ,000 | |||
| Ln_KTIC | ,037 | ,042 | ,106 | ,891 | ,382 | ||
| Ln_KHTIC | ,415 | ,054 | ,898 | 7,719 | ,000 | ||
| Ln_L | -,004 | ,010 | -,014 | -,415 | ,682 | ||
Tableau des coefficients du modèle Modèle Coefficients non standardisés Coefficients standardisés t
Sig. B Erreur standard Bêta (Constante) Ln_KTIC Ln_KHTIC Ln_L
 L’examen des résultats fournis par ce premier modèle nous donne les élasticités de la variable KTIC et L théoriquement non significatives et une valeur du test de Durbin-Watson qui ne permet pas de certifier l’inexistence d’auto-corrélation des erreurs. Pour cette raison nous avons jugé utile d’introduire une variable Dummy (binaire), afin de capter la volonté des pouvoirs publics en faveur du développement du secteur TIC au Maroc. Cette variable prend la valeur 0 entre 1980 et 1997 et 1 pour les autres années restantes. Ainsi en tenant compte de nos remarques, nous pouvons réécrire l’équation générique du modèle à estimer de la manière suivante En estimant à nouveau notre modèle par la méthode des moindres carrés ordinaires (MCO), nous obtenons les résultats suivants Tableau 13 Tableau des coefficients du modèle avec variable Dummy.
L’examen des résultats fournis par ce premier modèle nous donne les élasticités de la variable KTIC et L théoriquement non significatives et une valeur du test de Durbin-Watson qui ne permet pas de certifier l’inexistence d’auto-corrélation des erreurs. Pour cette raison nous avons jugé utile d’introduire une variable Dummy (binaire), afin de capter la volonté des pouvoirs publics en faveur du développement du secteur TIC au Maroc. Cette variable prend la valeur 0 entre 1980 et 1997 et 1 pour les autres années restantes. Ainsi en tenant compte de nos remarques, nous pouvons réécrire l’équation générique du modèle à estimer de la manière suivante En estimant à nouveau notre modèle par la méthode des moindres carrés ordinaires (MCO), nous obtenons les résultats suivants Tableau 13 Tableau des coefficients du modèle avec variable Dummy.
| Tableau des coefficients du Modèle rectifié | ||||||||
| Modèle | Coefficients non standardisés | Coefficients standardisés | t | Sig. | ||||
| A | Erreur standard | Bêta | ||||||
| (Constante) | 7,460 | ,288 | 25,892 | ,000 | ||||
| Ln_KTIC | ,076 | ,038 | ,217 | 2,014 | ,056 | |||
| Ln_KHTIC | ,322 | ,055 | ,696 | 5,882 | ,000 | |||
| Ln_L | ,000 | ,008 | ,002 | ,059 | ,953 | |||
| D_1998 | ,061 | ,020 | ,110 | 3,112 | ,005 | |||
| a. Variable dépendante : Ln_PIB | ||||||||
Tableau des coefficients du Modèle rectifié Modèle Coefficients non standardisés Coefficients standardisés t
Sig. A Erreur standard Bêta (Constante) Ln_KTIC Ln_KHTIC Ln_L D_1998 a. Variable dépendante Ln_PIB
D’où l’équation du modèle devient La valeur signifie qu’en moyenne, une augmentation de 1 % du capital TIC devrait se traduire par une augmentation de 7,56 % du PIB selon une certaine limite. En comparant les coefficients du modèle, nous remarquons qu’ils sont plus élevés pour la variable KHTIC que pour la variable TIC. On peut interpréter ce résultat de la manière suivante à un taux de croissance du facteur capital égal dans les deux secteurs, ce sont les investissements dans les secteurs hors TIC qui contribuent le plus à la croissance économique malgré le fait comme nous l’avions montré précédemment, que le secteur TIC soit devenu dynamique ces dernières années. Aussi constatons-nous que le coefficient du facteur travail L n’est pas significatif. Nous décidons quand même de maintenir ce modèle malgré cela car le modèle aurait pu donner des résultats très satisfaisants s’il était appliqué à un pays développé. En effet, des facteurs limitatifs peuvent être à la base de résultats non escomptés dans un pays en développement. Parmi ces facteurs, nous pouvons retenir l’analphabétisme ; ainsi une augmentation du capital dans le secteur TIC pourrait ne pas avoir un effet significatif du fait qu’une part importante de la population ne saurait faire bon usage de ces technologies. II.5. Validation du modèle II.5.1. Test statistique sur le modèle global En examinant le tableau de l’analyse de la variance ci dessous, Tableau 14 Tableau ANOVA du modèle.
| Tableau ANOVA | |||||||
| Modèle | Somme des carrés | ddl | Moyenne des carrés | F | Sig. | ||
| Régression | 1,737 | 4 | ,434 | 562,269 | ,000a | ||
| Résidu | ,017 | 22 | ,001 | ||||
| Total | 1,754 | 26 | |||||
| b. Variable dépendante : Ln_PIB | |||||||
Tableau ANOVA Modèle Somme des carrés ddl
Moyenne des carrés F Sig. Régression Résidu Totalb. Variable dépendante Ln_PIB
Nous constatons que le test d’hypothèse, Vs nous pousse à rejeter l’hypothèse au seuil car la statistique de Fisher-Snedecor observée est supérieure au fractile de la loi de Fisher-Snedecor lu sur la table au seuil d’où le modèle est globalement significatif, ceci par le fait que les variables Stock de capital TIC, Stock de capital hors TIC et le stock de travail engagé à l’échelle nationale (L) y compris la variable Dummy D_1998 sont globalement significatives. II.5.2. Test statistique sur les coefficients du modèle A partir des relations définies auparavant, le test statistique sur les coefficients du modèle, convient à calculer les ratios de student et de les comparer à la valeur lue dans la table au seuil 5% du fractile de student qui est égale a dans notre cas. Tableau 15 Tableau des coefficients du modèle avec intervalles de confiance des paramètres estimés
| Tableau des coefficients du modèle avec intervalles de confiance des paramètres estimés | ||||||||
| Modèle | Coefficients non standardisés | Coefficients standardisés | t | Sig. | 95,0% % intervalles de confiance pour B | |||
| A | Erreur standard | Bêta | Borne inférieure | Limite supérieure | ||||
| (Constante) | 7,460 | ,288 | 25,892 | ,000 | 6,862 | 8,058 | ||
| Ln_KTIC | ,076 | ,038 | ,217 | 2,014 | ,056 | -,002 | ,153 | |
| Ln_KHTIC | ,322 | ,055 | ,696 | 5,882 | ,000 | ,208 | ,435 | |
| Ln_L | ,000 | ,008 | ,002 | ,059 | ,953 | -,017 | ,018 | |
| D_1998 | ,061 | ,020 | ,110 | 3,112 | ,005 | ,020 | ,102 | |
Tableau des coefficients du modèle avec intervalles de confiance des paramètres estimés Modèle Coefficients non standardisés Coefficients standardisés t
Sig. intervalles de confiance pour B
A Erreur standard Bêta Borne inférieure Limite supérieure
D’après le tableau ci-dessus, nous obtenons: . Pour l’hypothèse Vs , on a on accepte l’hypothèse. D’où la variable Ln_KTIC ne contribue pas à l’explication de la variable Ln_Y. . Pour l’hypothèse Vs , on a on rejette l’hypothèse. D’où la variable Ln_KHTIC contribue à l’explication de la variable Ln_Y. . Pour l’hypothèse Vs , on a on accepte l’hypothèse. D’où la variable Ln_L ne contribue pas à l’explication de la variable Ln_Y . Pour l’hypothèse Vs , on a on accepte l’hypothèse. D’où la variable D_1998 contribue a l’explication de la variable Ln_Y. II.5.3. Test de détection d’une multi-colinéarité (test de Farrar et Glauber). Ce test revient à tester l’hypothèse (les séries sont orthogonales) Vs (les séries sont dépendantes).Avec D, le déterminant de la matrice des coefficients de corrélation des variables (Ln_KTIC, Ln_KHTIC, Ln_L et D_1998). Le calcul du déterminant D, nous donne = La valeur empirique de calculée à partir de l’échantillon est Nous allons comparer cette valeur au fractile de chi-deux à degré de liberté pour un seuil on ; on rejette l’hypothèse nulle. Ceci dit qu’il y a présomption de multi-colinéarité entre les variables explicatives. L’aboutissement à ce résultat est toujours dû aux limites du modèle pour un pays en développement, comme nous l’avons déjà mentionné plus haut. II.5.4. Coefficient de détermination Tableau 16 Tableau récapitulatif du modèle1.
| Modèle | R | R-deux | R-deux ajusté | Erreur standard de l’estimation |
| 1 | ,995a | ,990 | ,989 | ,02779 |
Modèle R R-deux R-deux ajusté Erreur standard de l’estimation
En examinant ce tableau, nous enregistrons un coefficient de détermination ; ceci peut s’expliquer par le fait que de variation totale du PIB est dû aux variables explicatives (KTIC, KHTIC, L et D_1998) et nous pouvons souligner que la qualité du modèle obtenu est relativement bonne. II.5.5. Test sur les résidus du modèle 1) Test d’autocorrélation des résidus statistique de Durbin-Watson Tableau 17 Test d’autocorrélation des résidus statistique de Durbin-Watson.
| Variable | Coefficient | Prob(F-statistic) |
| Durbin-Watson stat | 2.523108 | 0.000000 |
Variable Coefficient Prob(F-statistic) Durbin-Watson stat
La valeur de la statistique montre qu’il y a absence d’autocorrélation des résidus. 2) Test de normalité des résidusstatistique de Jarque Bera Figure 11 Test de normalité des résidus statistique de Jarque Bera. 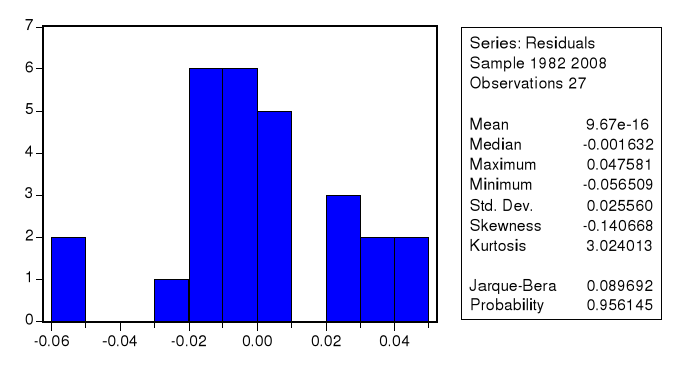 La probabilité de Jarque-Bera (0.956145) est supérieure à 5% ; cela implique que les résidus suivent une loi normale. 3) Test d’hétéroscédacticité des résidus test de White Tableau 18 Test d’hétéroscédacticité des résidus test de White.
La probabilité de Jarque-Bera (0.956145) est supérieure à 5% ; cela implique que les résidus suivent une loi normale. 3) Test d’hétéroscédacticité des résidus test de White Tableau 18 Test d’hétéroscédacticité des résidus test de White.
| White Heteroskedasticity Test: | ||||
| F-statistic | 1.039604 | Probability | 0.437108 | |
| Obs*R-squared | 7.477394 | Probability | 0.380919 | |
White Heteroskedasticity Test:
F-statistic Probability Obs*R-squared Probability
Les deux probabilités sont supérieures à 5% donc on accepte l’hypothèse d’homoscédasticité des erreurs. Les estimations obtenues par les moindres carrés ordinaires sont optimales. 4) Test de spécification Il existe plusieurs tests de spécification (Ramsey, etc). Ici, nous retenons le test de Ramsey. Le Reset13(*) teste les erreurs de spécification suivantes: · Omission des variables explicatives · Forme fonctionnelle incorrecte · Corrélation entre explicatives et termes d’erreurs dues entre autres à des erreurs de mesure, des termes retardés de l’endogène corrélés aux erreurs. Tableau 19 Test de spécification.
| Ramsey RESET Test: | |||
| F-statistic | 0.143676 | Probability | 0.708459 |
| Log likelihood ratio | 0.184097 | Probability | 0.667876 |
Ramsey RESET Test: F-statistic Probability Log likelihood ratio Probability
Les deux probabilités sont supérieures à 5% donc on accepte l’hypothèse Ho, le modèle est bien spécifié. 5) Test de Rendement d’échelle constant Ce test nous permet de tester si le PIB augmente dans une proportion identique aux facteurs de production ou pas. Dans ce cas nous allons tester l’hypothèse suivante VS La statistique de student calculée est donc égale, sous , à Or la matrice des variances covariances des coefficients est donnée par Tableau 20 Matrice des variances covariances des coefficients du modèle1.
| LN_PIB | LN_KTIC | LN_KHTIC | LN_L | |
| LN_PIB | 0.06494543 | 0.18126123 | 0.1396375 | 0.14069251 |
| LN_KTIC | 0.18126123 | 0.53275143 | 0.39370923 | 0.4222887 |
| LN_KHTIC | 0.1396375 | 0.39370923 | 0.30463681 | 0.30901201 |
| LN_L | 0.14069251 | 0.4222887 | 0.30901201 | 0.7666345 |
LN_PIB LN_KTIC LN_KHTIC LN_L LN_PIB LN_KTIC LN_KHTIC LN_L
Nous avons 60% de risque de rejeter l’hypothèse à tort, nous pouvons considérer le rendement d’échelle comme significativement croissant. D’où La production augmente plus vite que les facteurs de production. II.6. Présentation des résultats et interprétations contribution des TIC à la croissance Economique. On montre que la croissance de la production s’exprime relativement à la croissance des quantités de travail et du capital. Il est alors facile de raisonner en termes de contributions des facteurs. La croissance de la production est une somme pondérée de la croissance de la quantité de travail employée, de la quantité de capital utilisée, et d’un ensemble d’effets non liés à la variation des quantités de facteurs. Les deux premières composantes relèvent de la croissance extensive, la dernière de la croissance intensive. Cette dernière partie ne peut se mesurer que comme un résidu statistique. La dérivée logarithmique par rapport au temps d’une variable x est égale au rapport de la dérivée de x par rapport au temps et de x .Or cela est aussi égal au taux de croissance de cette variable. Partant alors de notre modèle initial on a
Aux fins d’application empirique, (X pouvant être égale à l’une des variable) sera approché par un taux de variation logarithmique14(*) Pour déterminer la contribution des TIC à la croissance marocaine, nous adoptons la démarche suivante ; soit la valeur de cette contribution, l’élasticité du PIB par rapport au facteur capital TIC (c’est-à-dire que u représente a1) et le taux de croissance de ce facteur (c’est-à-dire que ð représente =; on vérifie que. L’application de cette relation fait apparaître que pour la période 1998-2008, la contribution du secteur des TIC à la croissance économique au Maroc est de l’ordre de 6%. En effet, d’après notre modèle . Les valeurs respectives de KTIC2008 et KTIC1998 (k=10) étant de 25987 et 12433, le log de leur rapport est 0,74 .Ainsi, le produit donne sensiblement 0,06. L’obtention de cette valeur considérable témoigne de l’efficacité des actions entreprises par les pouvoirs publics à partir de la période 1998-2008. Lire le mémoire complet ==> (L’impact des TIC sur le tissu productif des biens et services) Projet de Fin d’Etudes – Option : Statistique Haut Commissariat au Plan – Institut National de Statistique et d’Economie Appliquee
